题目内容
已知{xn}是公差为d（d＞0）的等差数列，
的前n项的平均数．（1）证明数列
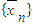也是等差数列，并指出公差；（2）记{xn}的前n项和为Sn，
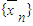的前n项和为
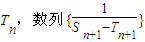的前n项和为Un，求证：
．
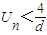【答案】分析：（1）由
的前n项的平均数，知
，由数列的性质知
=
，整理得
=
，所以{
}是以x1为首项，以
为公差的等差数列．
（2）由
，知
，所以
，由此能够证明
．
解答：证明：（1）∵
=
=
=
，
∴{
}是以x1为首项，以
为公差的等差数列．
（2）∵
，
，
∴
，
∴
=
，
∴
=
．
点评：本题考查等差数列的证明和前n项和的求法，是基础题．解题时要认真审题，仔细解答，注意算术平均数的应用．
的前n项的平均数，知，由数列的性质知=，整理得=，所以{}是以x1为首项，以为公差的等差数列．（2）由
，知，所以，由此能够证明．解答：证明：（1）∵
=
=
=
，∴{
}是以x1为首项，以为公差的等差数列．（2）∵
，，∴
，∴
=
，∴
=
．点评：本题考查等差数列的证明和前n项和的求法，是基础题．解题时要认真审题，仔细解答，注意算术平均数的应用．
练习册系列答案
开心练习课课练与单元检测系列答案
相关题目
已知{xn}是公差为d的等差数列，
(x1+x2+…+xn)；
表示{xn}的前n项的平均数．
是等差数列，指出公差．
的前n项和为Tn，
的前n项和为Un．若d≠0，求
．