题目内容
已知{xn}是公差为d(d>0)的等差数列,
n表示{xn}的前n项的平均数.
(1)证明数列{
n}也是等差数列,并指出公差;
(2)记{xn}的前n项和为Sn,{
n}的前n项和为Tn,数列{
}的前n项和为Un,求证:Un<
.
. |
| x |
(1)证明数列{
. |
| x |
(2)记{xn}的前n项和为Sn,{
. |
| x |
| 1 |
| S n+1-Tn+1 |
| 4 |
| d |
分析:(1)由
n表示{xn}的前n项的平均数,知
=
,由数列的性质知
=
,整理得
=x1+(n-1)•
,所以{
}是以x1为首项,以
为公差的等差数列.
(2)由Sn=nx1+
•d,知Tn=n x1+
•
,所以Sn-Tn=
d,由此能够证明Un<
.
. |
| x |
. |
| xn |
| x1+x2+…+xn |
| n |
. |
| xn |
| Sn |
| n |
. |
| xn |
| d |
| 2 |
. |
| xn |
| d |
| 2 |
(2)由Sn=nx1+
| n(n-1) |
| 2 |
| n(n-1) |
| 2 |
| d |
| 2 |
| n(n-1) |
| 4 |
| 4 |
| d |
解答:证明:(1)∵
=
=
=
=x1+(n-1)•
,
∴{
}是以x1为首项,以
为公差的等差数列.
(2)∵Sn=nx1+
•d,
Tn=n x1+
•
,
∴Sn-Tn=
d,
∴
=
•
=
•(
-
),
∴Un=
[(1-
)+(
-
)+(
-
)+…+(
-
)]
=
(1-
)<
.
. |
| xn |
| x1+x2+…+xn |
| n |
=
| Sn |
| n |
=
nx1+
| ||
| n |
=x1+(n-1)•
| d |
| 2 |
∴{
. |
| xn |
| d |
| 2 |
(2)∵Sn=nx1+
| n(n-1) |
| 2 |
Tn=n x1+
| n(n-1) |
| 2 |
| d |
| 2 |
∴Sn-Tn=
| n(n-1) |
| 4 |
∴
| 1 |
| Sn+1-Tn+1 |
| 4 |
| d |
| 1 |
| n(n+1) |
=
| 4 |
| d |
| 1 |
| n |
| 1 |
| n+1 |
∴Un=
| 4 |
| d |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
=
| 4 |
| d |
| 1 |
| n+1 |
| 4 |
| d |
点评:本题考查等差数列的证明和前n项和的求法,是基础题.解题时要认真审题,仔细解答,注意算术平均数的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
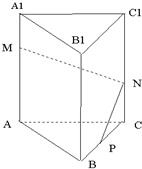 已知{xn}是公差为d的等差数列,
已知{xn}是公差为d的等差数列, 的前n项的平均数.
的前n项的平均数.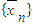 也是等差数列,并指出公差;
也是等差数列,并指出公差;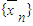 的前n项和为
的前n项和为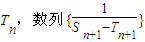 的前n项和为Un,求证:
的前n项和为Un,求证: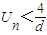 .
. 表示{xn}的前n项的平均数.
表示{xn}的前n项的平均数. 是等差数列,指出公差.
是等差数列,指出公差. 的前n项和为Tn,
的前n项和为Tn, 的前n项和为Un.若d≠0,求
的前n项和为Un.若d≠0,求 .
.