题目内容
7.在锐角三角形ABC中,角A、B、C的对边分别为a、b、c,$\sqrt{3}a=2csinA$.(1)求角C;
(2)若c=7,且△ABC的面积为$10\sqrt{3}$,求△ABC的周长.
分析 (1)利用正弦定理求解即可.
(2)利用余弦定理以及三角形的面积,求解三角形的周长即可.
解答 解:(1)由$\sqrt{3}a=2csinA$和$\frac{a}{sinA}=\frac{c}{sinC}$得,$sinC=\frac{{\sqrt{3}}}{2}$…(3分)
因为$0<C<\frac{π}{2}$,所以$C=\frac{π}{3}$…(5分)
(2)由余弦定理a2+b2-2abcosC=c2得,a2+b2-ab=49…(7分)
由△ABC的面积为$10\sqrt{3}$得,$\frac{1}{2}absinC=10\sqrt{3}$,ab=40…(9分)
所以a2+b2+2ab=(a2+b2-ab)+3ab=169,a+b=13…(11分)
△ABC的周长为a+b+c=20…(12分)
点评 本题考查正弦定理以及余弦定理的应用,考查计算能力.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
15.若连续抛掷两次骰子得到的点数分别为m,n,则点P(m,n)在函数y=-x+4图象上的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{12}$ |
2.命题“若α=0,则sinα<cosα”的否命题是( )
| A. | 若α=0,则sinα≥cosα | B. | 若sinα<cosα,则α≠0 | ||
| C. | 若α≠0,则sinα≥cosα | D. | 若sinα≥cosα,则α≠0 |
12.设α,β是两个不同的平面,直线m⊥α,则“m⊥β”是“α∥β”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
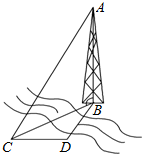 如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.
如图,测量河对岸的塔高AB时,选与塔底B在同一水平面内的两个测点C与D,在D点测得塔在北偏东30°方向,然后向正西方向前进10米到达C,测得此时塔在北偏东60°方向.并在点C测得塔顶A的仰角为60°,则塔高AB=30米.