题目内容
16.已知实数x、y满足不等式$\left\{\begin{array}{l}{x+3y≥3}\\{2x-y-3≤0}\\{x-my+1≥0}\end{array}\right.$,若目标函数z=x+y最大值为9,求实数m的值.分析 作出可行域,变形目标函数,平移直线y=-x可知当直线经过点C时,目标函数取最大值,联立$\left\{\begin{array}{l}{2x-y-3=0}\\{x-my+1=0}\end{array}\right.$可解得C的坐标,解m的方程可得.
解答 解:由题意作出不等式$\left\{\begin{array}{l}{x+3y≥3}\\{2x-y-3≤0}\\{x-my+1≥0}\end{array}\right.$所对应的可行域(如图△ABC)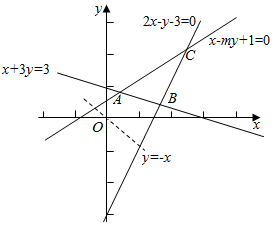 ,
,
变形目标函数可得y=-x+z,平移直线y=-x可知当直线经过点C时,目标函数取最大值,
联立$\left\{\begin{array}{l}{2x-y-3=0}\\{x-my+1=0}\end{array}\right.$可解得C($\frac{3m+1}{2m-1}$,$\frac{5}{2m-1}$),
故$\frac{3m+1}{2m-1}$+$\frac{5}{2m-1}$=9,解方程可得m=1.
点评 本题考查简单线性规划,准确作图并数形结合是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.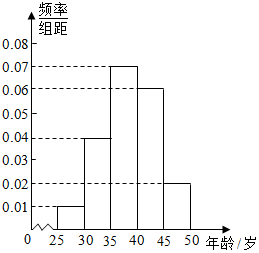 某iphone手机专卖店对某市市民进行iphone手机认可度的调查,在已购买iPhone手机的1000名市民中随机抽取100名,按年龄(单位:岁)进行统计的频率分布表和频率分布直方图如下:
某iphone手机专卖店对某市市民进行iphone手机认可度的调查,在已购买iPhone手机的1000名市民中随机抽取100名,按年龄(单位:岁)进行统计的频率分布表和频率分布直方图如下:
(1)求频数分布表中x,y的值;
(2)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加iphone手机宣传活动,现从这20人中随机选取2人各赠送一部iphone6s手机,设这2名市民中年龄在[40,45)内的人数为X,求X的分布列及数学期望.
 某iphone手机专卖店对某市市民进行iphone手机认可度的调查,在已购买iPhone手机的1000名市民中随机抽取100名,按年龄(单位:岁)进行统计的频率分布表和频率分布直方图如下:
某iphone手机专卖店对某市市民进行iphone手机认可度的调查,在已购买iPhone手机的1000名市民中随机抽取100名,按年龄(单位:岁)进行统计的频率分布表和频率分布直方图如下:| 分组(岁) | 频数 |
| [25,30) | 5 |
| [30,35) | x |
| [35,40) | 35 |
| [40,45) | y |
| [45,50] | 10 |
| 合计 | 100 |
(2)在抽取的这100名市民中,按年龄进行分层抽样,抽取20人参加iphone手机宣传活动,现从这20人中随机选取2人各赠送一部iphone6s手机,设这2名市民中年龄在[40,45)内的人数为X,求X的分布列及数学期望.
4.M={x|5-x≥$\sqrt{2(x-1)}$},N={x|x2-ax≤x-a},当M?N时,a的取值范围是( )
| A. | a≥3 | B. | a≤3 | C. | a<3 | D. | a>3 |
8.已知sinθ=$\frac{m-3}{m+5}$,cosθ=$\frac{4-2m}{m+5}$,其中$\frac{π}{2}$<θ<π,则tanθ=( )
| A. | -$\sqrt{2}$ | B. | -$\frac{12}{5}$ | C. | -2 | D. | -$\frac{5}{12}$ |
8.已知椭圆C1:$\frac{x^2}{{{a_1}^2}}+\frac{y^2}{{{b_1}^2}}=1({a_1}>{b_1}>0)$与双曲线C2:$\frac{x^2}{{{a_2}^2}}-\frac{y^2}{{{b_2}^2}}=1({a_2}>0,{b_2}>0)$有相同的焦点F1,F2,点P是两曲线的一个公共点,且PF1⊥PF2,e1,e2分别是两曲线C1,C2的离心率,当4e12+e22取得最小值时,C1的离心率e1等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{3}$ |
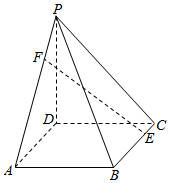 如图,四棱锥P-ABCD的底面ABCD是菱形,侧棱PD⊥底面ABCD,∠BCD=60°.
如图,四棱锥P-ABCD的底面ABCD是菱形,侧棱PD⊥底面ABCD,∠BCD=60°.