题目内容
在直线l:3x-y-1=0上求一点P,使得P到A(4,1)和B(0,4)的距离之差最大;
如图1,设点B关于l的对称点B′的坐标为(a,b),直线l的斜率为k1,则k1·kBB′=-1.即3·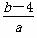 =-1.
=-1.
∴a+3b-12=0.①
又由于线段BB′的中点坐标为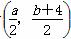 ,且在直线l上,
,且在直线l上,
∴3× -
-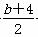 -1=0.即3a-b-6=0.②
-1=0.即3a-b-6=0.②
解①②得a=3,b=3,∴B′(3,3).
于是AB′的方程为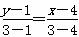 ,即2x+y-9=0.
,即2x+y-9=0.
解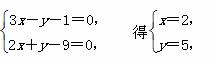
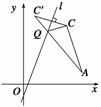 即l与AB′的交点坐标为P(2,5).
即l与AB′的交点坐标为P(2,5).

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案
相关题目
 在点(1,1)处的切线与
在点(1,1)处的切线与 轴的交点的横坐标为
轴的交点的横坐标为 ,
, 的值为
的值为  的倾斜角
的倾斜角 的大小是___ __.
的大小是___ __.  的中线
的中线 与中位线
与中位线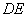 相交于
相交于 ,已知
,已知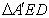 是△
是△ 绕
绕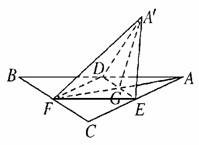 A.动点
A.动点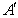 在平面
在平面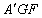 ⊥平面
⊥平面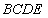
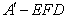 的体积有最大值
的体积有最大值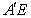 与
与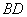 不可能垂直
不可能垂直