题目内容
点P是圆x2+y2=16上的一个动点,过点P作PD垂直于x轴,垂足为D,Q为线段PD的中点.
(1)求点Q的轨迹方程.
(2)若经过点(-1,1)的直线与Q点轨迹有两个不同交点,求直线斜率的取值范围.
解:由题意,令Q(x,y),P(s,t),
由于点P是圆x2+y2=16上的一个动点,过点P作PD垂直于x轴,垂足为D,Q为线段PD的中点
∴s=x,t=2y,又点P是圆x2+y2=16上的一个动点
∴x2+4y2=16,即为点Q的轨迹方程
(2)由(1)点Q的轨迹是椭圆
由于点(-1,1)一定在椭圆内,故过点点的直线一定与椭圆有两个交点
所以此直线的斜率的取值范围是R
分析:(1)由题意点P是圆x2+y2=16上的一个动点,过点P作PD垂直于x轴,垂足为D,Q为线段PD的中点,可得点Q的坐标与点P的坐标的关系,用中点Q的坐标表示出点P的坐标,然后再代入圆的方程求出点Q的轨迹方程
(2)由(1)点Q的轨迹是一个椭圆,由于点(-1,1)在椭圆的内部,过点(-1,1)的直线与椭圆一定有两个交点,故可得k∈R
点评:本题考查直线与圆方程的应用,解答本题关键点有二,一是熟练掌握代入法求轨迹方程,二是确定点(-1,1)在椭圆的内部,从而判断出直线斜率的取值范围,本题考查了推理判断的能力及代入法求轨迹方程技巧.
由于点P是圆x2+y2=16上的一个动点,过点P作PD垂直于x轴,垂足为D,Q为线段PD的中点
∴s=x,t=2y,又点P是圆x2+y2=16上的一个动点
∴x2+4y2=16,即为点Q的轨迹方程
(2)由(1)点Q的轨迹是椭圆

由于点(-1,1)一定在椭圆内,故过点点的直线一定与椭圆有两个交点
所以此直线的斜率的取值范围是R
分析:(1)由题意点P是圆x2+y2=16上的一个动点,过点P作PD垂直于x轴,垂足为D,Q为线段PD的中点,可得点Q的坐标与点P的坐标的关系,用中点Q的坐标表示出点P的坐标,然后再代入圆的方程求出点Q的轨迹方程
(2)由(1)点Q的轨迹是一个椭圆,由于点(-1,1)在椭圆的内部,过点(-1,1)的直线与椭圆一定有两个交点,故可得k∈R
点评:本题考查直线与圆方程的应用,解答本题关键点有二,一是熟练掌握代入法求轨迹方程,二是确定点(-1,1)在椭圆的内部,从而判断出直线斜率的取值范围,本题考查了推理判断的能力及代入法求轨迹方程技巧.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
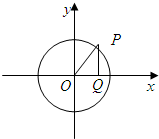 已知点P是圆x2+y2=1上的一个动点,过点P作PQ⊥x轴于点Q,设
已知点P是圆x2+y2=1上的一个动点,过点P作PQ⊥x轴于点Q,设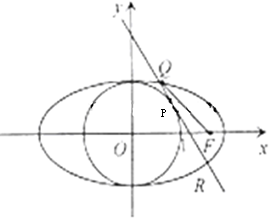 已知椭圆C:
已知椭圆C: