题目内容
已知点P是圆x2+y2=4上一动点,定点Q(4,0).(1)求线段PQ中点的轨迹方程;
(2)设∠POQ的平分线交PQ于R,求R点的轨迹方程.
分析:(1)设PQ中点M(x,y),则P(2x-4,2y),代入圆的方程即得线段PQ中点的轨迹方程.
(2)设R(x,y),由三角形角平分线性质得出一个比例式,再设P(m,n),得出关于m,n与x,y的关系式,代入x2+y2=4中,即得R点的轨迹方程.
(2)设R(x,y),由三角形角平分线性质得出一个比例式,再设P(m,n),得出关于m,n与x,y的关系式,代入x2+y2=4中,即得R点的轨迹方程.
解答:解:(1)设PQ中点M(x,y),则P(2x-4,2y),代入圆的方程得(x-2)2+y2=1.
(2)设R(x,y),由
=
=
,
设P(m,n),则有m=
,n=
,
代入x2+y2=4中,得
(x-
)2+y2=
(y≠0).
(2)设R(x,y),由
| |PR| |
| |RQ| |
| |OP| |
| |OQ| |
| 1 |
| 2 |
设P(m,n),则有m=
| 3x-4 |
| 2 |
| 3y |
| 2 |
代入x2+y2=4中,得
(x-
| 4 |
| 3 |
| 16 |
| 9 |
点评:求曲线的轨迹方程常采用的方法有直接法、定义法、相关点代入法、参数法,本题主要是利用直接法和相关点代入法,直接法是将动点满足的几何条件或者等量关系,直接坐标化,列出等式化简即得动点轨迹方程.相关点代入法 根据相关点所满足的方程,通过转换而求动点的轨迹方程.

练习册系列答案
相关题目
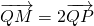 的点M的轨迹为曲线C.
的点M的轨迹为曲线C. 的点M的轨迹为曲线C.
的点M的轨迹为曲线C.