题目内容

精英家教网已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的右焦点F（
3
，0），长轴长为4．
（1）求椭圆C的方程，
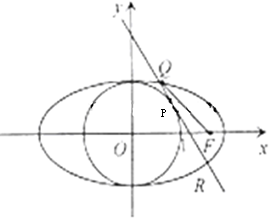
（2）点P是圆x2+y2=b2上第一象限内的任意一点，过P作圆的切线与椭圆C交于Q（x1，y1），R（x2，y2）（y1＞y2）两点．①求证：|PQ|+|FQ|=2．②求|QR|的最大值．
分析：（1）由题意可得c=
3
，2a=4，再利用b=
a2-c2
=1，即可得到椭圆C的方程．
（2）由于点Q（x1，y1）在椭圆上，可得
x
2
1
4
+
y
2
1
=1，利用两点间的距离公式可得|QF|=
(x1-
3
)2+
y
2
1
．利用切线的性质和勾股定理可得|PQ|=
|OQ|2-|OP|2
，即可得出|PQ|+|QF|=2．
②同理可得|PR|+|RF|=2．于是|QR|+|QF|+|FR|=4，利用三角形三边的关系可得|QR|≤|QF|+|FR|，可得当QR过点F时取最大值2．
解答：解：（1）由题意可得c=
3
，2a=4，
∴a=2，b=
a2-c2
=1，
∴椭圆C的方程为
x2
4
+y2=1．
（2）∵点Q（x1，y1）在椭圆上，∴
x
2
1
4
+
y
2
1
=1，
∴|QF|=
(x1-
3
)2+
y
2
1
=
(x1-
3
)2+1-
x
2
1
4
=
(
3
2
x1-2)2
=2-
3
2
x1．
|PQ|=
|OQ|2-|OP|2
=
x
2
1
+
y
2
1
-1
=
x
2
1
-
x
2
1
4
=
3
2
x1，
∴|PQ|+|QF|=2．
②同理可得|PR|+|RF|=2．
则|QR|+|QF|+|FR|=4，又|QR|≤|QF|+|FR|，
∴2|QR|≤4，即|QR|≤2．
∴当QR过点F时取最大值2．
点评：本题综合考查了椭圆的标准方程及其性质、两点间的距离公式、圆的切线的性质、勾股定理、三角形三边大小关系等基础知识与基本技能方法，属于难题．
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率为
1
2
，且经过点P(1，
3
2
)．
（1）求椭圆C的方程；
（2）设F是椭圆C的左焦，判断以PF为直径的圆与以椭圆长轴为直径的圆的位置关系，并说明理由．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的短轴长为2
3
，右焦点F与抛物线y2=4x的焦点重合，O为坐标原点．
（1）求椭圆C的方程；
（2）设A、B是椭圆C上的不同两点，点D（-4，0），且满足
DA
=λ
DB
，若λ∈[
3
8
，
1
2
]，求直线AB的斜率的取值范围．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）经过点A（1，
3
2
），且离心率e=
3
2
．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过点B（-1，0）能否作出直线l，使l与椭圆C交于M、N两点，且以MN为直径的圆经过坐标原点O．若存在，求出直线l的方程；若不存在，说明理由．
（2012•房山区二模）已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的长轴长是4，离心率为
1
2
．
（Ⅰ）求椭圆方程；
（Ⅱ）设过点P（0，-2）的直线l交椭圆于M，N两点，且M，N不与椭圆的顶点重合，若以MN为直径的圆过椭圆C的右顶点A，求直线l的方程．
已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的短轴长为2，离心率为
2
2
，设过右焦点的直线l与椭圆C交于不同的两点A，B，过A，B作直线x=2的垂线AP，BQ，垂足分别为P，Q．记λ=
AP+BQ
PQ
，若直线l的斜率k≥
3
，则λ的取值范围为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网