题目内容
sinA|=|sinB|是sin(A+B)=0的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要
B
分析:通过举反例判断出|sinA|=|sinB|成立时推不出sin(A+B)=0成立,反之,若sin(A+B)=0成立,能推出|sinA|=|sinB|成立,利用充要条件的有关定义得到结论.
解答:若|sinA|=|sinB|成立,例如A=B= ,满足|sinA|=|sinB|,但sin(A+B)=
,满足|sinA|=|sinB|,但sin(A+B)=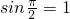 ,即推不出sin(A+B)=0,
,即推不出sin(A+B)=0,
反之,若sin(A+B)=0成立,则有A+B=kπ,所以A=kπ-B,所以sinA=sin(kπ-B),所以sinA=±sinB,
所以|sinA|=|sinB|成立,所以|sinA|=|sinB|是sin(A+B)=0的必要不充分条件,
故选B.
点评:本题考查判断一命题天是另一个命题的什么条件,应该两边互推一下,然后利用充要条件的有关定义进行判断,属于基础题.
分析:通过举反例判断出|sinA|=|sinB|成立时推不出sin(A+B)=0成立,反之,若sin(A+B)=0成立,能推出|sinA|=|sinB|成立,利用充要条件的有关定义得到结论.
解答:若|sinA|=|sinB|成立,例如A=B=
 ,满足|sinA|=|sinB|,但sin(A+B)=
,满足|sinA|=|sinB|,但sin(A+B)=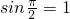 ,即推不出sin(A+B)=0,
,即推不出sin(A+B)=0,反之,若sin(A+B)=0成立,则有A+B=kπ,所以A=kπ-B,所以sinA=sin(kπ-B),所以sinA=±sinB,
所以|sinA|=|sinB|成立,所以|sinA|=|sinB|是sin(A+B)=0的必要不充分条件,
故选B.
点评:本题考查判断一命题天是另一个命题的什么条件,应该两边互推一下,然后利用充要条件的有关定义进行判断,属于基础题.

练习册系列答案
相关题目