题目内容
在△ABC中,已知tanB=| cos(C-B) | sinA+sin(C-B) |
分析:切和弦共同存在的等式中,一般要切化弦,根据两外项之积等于两内项之积,把分式化为整式,移项,逆用两角和的余弦公式,把脚C化为A+B用两角和的余弦公式展开,合并同类项,得到两角余弦乘积为零,则两角中必有一个直角.
解答:解:由已知得:
=
,
∴sinAsinB+sinBsin(C-B)=cosBcos(C-B),
移项,逆用两角和的余弦公式得:
sinAsinB=cosC,
∵在△ABC中,cosC=-cos(A+B),
∴sinAsinB=-cos(A+B),
∴cosAcosB=0,γ
∴cosA=0或 cosB=0,
∴△ABC是直角三角形.
| sinB |
| cosB |
| cos(C-B) |
| sinA+sin(C-B) |
∴sinAsinB+sinBsin(C-B)=cosBcos(C-B),
移项,逆用两角和的余弦公式得:
sinAsinB=cosC,
∵在△ABC中,cosC=-cos(A+B),
∴sinAsinB=-cos(A+B),
∴cosAcosB=0,γ
∴cosA=0或 cosB=0,
∴△ABC是直角三角形.
点评:和三角形有关的三角恒等变形,要求能用所有的公式特别是余弦的和差角公式 进行简单的三角函数式的化简、求值及恒等式的证明

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 )
) ,H是△ABC的垂心,且
,H是△ABC的垂心,且 .
. 的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.
的直线与轨迹M交于点P,点Q(t,0)是x轴上任意一点,求当△CPQ为锐角三角形时t的取值范围.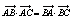 .
. |=|
|=| |;
|; ,求|
,求| -t
-t