题目内容
已知D为△ABC内的一点,AB=AC=1,∠BAC=63°,∠BAD=33°,∠ABD=27°,求DC(精确到小数点后两位,sin27°=0.4540).
【答案】分析:结合题意,在△ADC中,若AD可求,则DC可求,而AD可在△ABD中利用正弦定理求得.
解答:解:∠ADB=180°-(33°+27°)=120°,
根据正弦定理,得 ,
,
又∠CAD=63°-33°=30°,
由余弦定理可得
DC2=AD2+AC2-AD•AC•cos30°
=
= .
.
∴ .
.
点评:此题在求解过程中,先用正弦定理求边,再用余弦定理求边,体现了正、余弦定理的综合运用.
解答:解:∠ADB=180°-(33°+27°)=120°,
根据正弦定理,得
 ,
,又∠CAD=63°-33°=30°,
由余弦定理可得
DC2=AD2+AC2-AD•AC•cos30°
=

=
 .
.∴
 .
.点评:此题在求解过程中,先用正弦定理求边,再用余弦定理求边,体现了正、余弦定理的综合运用.

练习册系列答案
相关题目
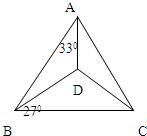 已知D为△ABC内的一点,AB=AC=1,∠BAC=63°,∠BAD=33°,∠ABD=27°,求DC(精确到小数点后两位,sin27°=0.4540).
已知D为△ABC内的一点,AB=AC=1,∠BAC=63°,∠BAD=33°,∠ABD=27°,求DC(精确到小数点后两位,sin27°=0.4540).