题目内容
已知D为△ABC的边BC的中点，△ABC所在平面内有一点P，满足| PA |
| BP |
| CP |
|
| ||
|
|
分析：由
+
+
=0，变形得
=
+
由向量加法的平行四边形法则知，PA必为以PB，PC为邻边的平行四边形的对角线，故有P，D，A三点共线，由平行四边形对角线的性质易得λ的值
| PA |
| BP |
| CP |
| PA |
| PB |
| PC |
解答：解：由
+
+
=0，变形得
=
+
由向量加法的平行四边形法则知，PA必为以PB，PC为邻边的平行四边形的对角线，
又D是BC的中点，故P，D，A三点共线，且D是PA的中点
又
=λ，故λ=2
故答案为2
| PA |
| BP |
| CP |
| PA |
| PB |
| PC |
又D是BC的中点，故P，D，A三点共线，且D是PA的中点
又
|
| ||
|
|
故答案为2
点评：本题考查向量的几何意义，由向量的关系得到几何图形中的位置关系，向量关系表示几何关系是向量的重要应用．
练习册系列答案
相关题目
已知D为△ABC的边AC的中点，若
•
=
•
，则△ABC的形状必为（ ）
| BD |
| BC |
| BA |
| BD |
| A、等边三角形 |
| B、直角三角形 |
| C、等腰三角形 |
| D、等腰直角三角形 |
：1．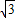
，且∠ADC=45°，求BD的长．