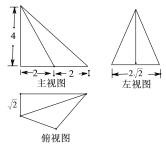
题目内容
【题目】如图，在极坐标系
中，
，
，
，
，
，弧
，
所在圆的圆心分别是
，
，曲线
是弧，曲线
是线段
，曲线
是线段
，曲线
是弧.
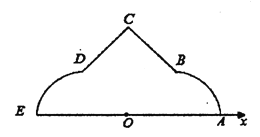
（1）分别写出，，，的极坐标方程；
（2）曲线
由，，，构成，若点
，（
），在上，则当
时，求点
的极坐标.
【答案】（1）线
的极坐标方程为：
，
的极坐标方程为：
，
，的极坐标方程分别为：
，
；（2）
，
.
【解析】
（1）在极坐标系下，在曲线上任取一点
，直角三角形
中，
，曲线的极坐标方程为：，同理可得其他.
（2）当
时，
，
，当
，
，
计算得到答案.
（1）解法一：在极坐标系下，在曲线上任取一点，连接
、
，
则在直角三角形中，
，
，
，得：.
所以曲线的极坐标方程为：
又在曲线上任取一点，则在
中，，
，，
，
，由正弦定理得：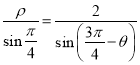
，
即：
，化简得的极坐标方程为：
同理可得曲线，的极坐标方程分别为：，
解法二：（先写出直角坐标方程，再化成极坐标方程.）
由题意可知，，，的直角坐标方程为：
，
，
，
，
所以，，，的极坐标方程为：，
，
，
（2）当时，，，
当时，，，
所以
点的极坐标为，
练习册系列答案
小学学习好帮手系列答案
小学同步三练核心密卷系列答案
相关题目
