题目内容
【题目】已知椭圆![]() 的中心在坐标原点
的中心在坐标原点![]() ,其右焦点为
,其右焦点为![]() ,以坐标原点
,以坐标原点![]() 为圆心,椭圆短半轴长为半径的圆与直线
为圆心,椭圆短半轴长为半径的圆与直线![]() 相切.
相切.
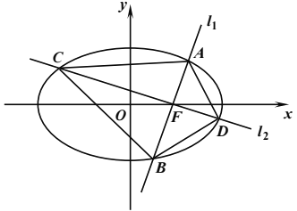
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)经过点![]() 的直线
的直线![]() ,
,![]() 分别交椭圆
分别交椭圆![]() 于
于![]() ,
,![]() 及
及![]() ,
,![]() 四点,且
四点,且![]() ,探究:是否存在常数
,探究:是否存在常数![]() ,使得
,使得![]() .
.
【答案】(1)![]() (2)
(2)![]() ,使得
,使得![]() 恒成立.
恒成立.
【解析】
(Ⅰ)根据点到直线的距离公式得到![]() ,再由a,b,c的关系可得到每一个参数值;(Ⅱ)(ⅰ)当
,再由a,b,c的关系可得到每一个参数值;(Ⅱ)(ⅰ)当![]() 与
与![]() 其中一条直线的斜率不存在时,易知
其中一条直线的斜率不存在时,易知![]() ,
,![]() 其中一个为长轴,另一个为通径,可代入验证,求得参数值;(ⅱ)当
其中一个为长轴,另一个为通径,可代入验证,求得参数值;(ⅱ)当![]() 与
与![]() 斜率存在且不为零时,设
斜率存在且不为零时,设![]() 的方程为
的方程为![]() ,则
,则![]() 的方程
的方程![]() ,分别联立两直线和椭圆方程,结合弦长公式和韦达定理得到参数值.
,分别联立两直线和椭圆方程,结合弦长公式和韦达定理得到参数值.
(Ⅰ)设所求椭圆![]() 的方程为
的方程为![]() ,
,
由点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,故
,故![]() ,
,
又![]() ,所以
,所以![]() ,
,
故所求椭圆![]() 的方程为
的方程为![]() ;
;
(Ⅱ) 假设存在常数![]() ,使得
,使得![]() 恒成立,则
恒成立,则![]() ,
,
(ⅰ)当![]() 与
与![]() 其中一条直线的斜率不存在时,易知
其中一条直线的斜率不存在时,易知![]() ,
,![]() 其中一个为长轴,另一个为通径,长轴长为
其中一个为长轴,另一个为通径,长轴长为![]() ,通径为
,通径为![]() ,
,
此时![]() ,
,
(ⅱ)当![]() 与
与![]() 斜率存在且不为零时,不妨设
斜率存在且不为零时,不妨设![]() 的方程为
的方程为![]() ,
,
则![]() 的方程
的方程![]() ,联立方程
,联立方程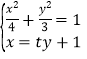 ,消去
,消去![]() 可得
可得
![]() ,设
,设![]() ,
,![]() ,
,
则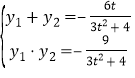
![]() ,所以
,所以
![]()
![]() ,
,
将![]() 代入,化简可得
代入,化简可得![]() ,
,
在![]() 的表达式中用“
的表达式中用“![]() ”代“
”代“![]() ”可得
”可得![]() ,
,
所以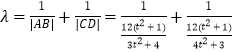
![]() .
.
综合(ⅰ)(ⅱ)可知存在常数![]() ,使得
,使得![]() 恒成立.
恒成立.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
【题目】如图,![]() 地到火车站共有两条路径,据统计两条路径所用的时间互不影响,所用时间在各时间段内的的频率如下表:
地到火车站共有两条路径,据统计两条路径所用的时间互不影响,所用时间在各时间段内的的频率如下表:
时间(分钟) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
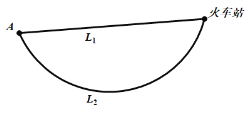
现甲、乙两人分别有![]() 分钟和
分钟和![]() 分钟时间用于赶往火车站.
分钟时间用于赶往火车站.
(1)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
(2)用![]() 表示甲、乙两人中在允许的时间内赶到火车站的人数,针对(1)的选择方案,求
表示甲、乙两人中在允许的时间内赶到火车站的人数,针对(1)的选择方案,求![]() 的分布列和数学期望.
的分布列和数学期望.