题目内容
已知抛物线y2＝4x截直线y＝2x＋m所得弦长AB＝3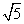
，
(1)求m的值；
(2)设P是x轴上的一点，且△ABP的面积为9，求P的坐标．
故点P的坐标为(5,0)或(－1,0)．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
口算题卡加应用题集训系列答案综合自测系列答案题目内容
已知抛物线y2＝4x截直线y＝2x＋m所得弦长AB＝3，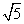
(1)求m的值；
(2)设P是x轴上的一点，且△ABP的面积为9，求P的坐标．
故点P的坐标为(5,0)或(－1,0)．
口算题卡加应用题集训系列答案综合自测系列答案
所表示的曲线是( )
＋
＝1(0<b<2)，左、右焦点分别为F1，F2，过F1的直线l交椭圆于A，B两点，若|BF2|＋|AF2|的最大值为5，则b的值是( )
D.
－
＝1(a>0，b>0)的左焦点，点E是该双曲线的右顶点，过点F且垂直于x轴的直线与双曲线交于A，B两点，若△ABE是锐角三角形，则该双曲线的离心率e的取值范围是( )
，2)
，2) D．(2,3)
的值一定等于( )
，圆O：x2＋y2＝5，椭圆E：
＋
＝1(a>b>0)的离心率e＝
，直线l被圆O截得的弦长与椭圆的短轴长相等．
