题目内容
17．若函数f（x）=x4+2x3+4x2+cx的图象关于直线x=m对称，则f（x）的最小值是-$\frac{11}{16}$．分析 根据函数f（x）=x4+2x3+4x2+cx的图象关于直线x=m对称，可得m=$\frac{1}{2}$，进而得到c=3，进而可得f（x）=x4+2x3+4x2+3x=（x2+x）（x2+x+3）=[（x2+x）+$\frac{3}{2}$]2-$\frac{9}{4}$，结合二次函数的图象和性质，可得答案．
解答 解：一般地，四次函数f（x）=（x-a）（x-b）（x-c）（x-d）
=x4+（a+b+c+d）x3+mx2+nx+abcd的图象，关于直线x=$\frac{1}{4}$（a+b+c+d）对称，
故函数f（x）=x4+2x3+4x2+cx的图象关于直线x=$\frac{1}{2}$对称，
由函数解析式的常数项为0，可得函数有一零点为0，
则-1也必为函数的一个零点，
故c=3，
∴函数f（x）=x4+2x3+4x2+3x=（x2+x）（x2+x+3）=[（x2+x）+$\frac{3}{2}$]2-$\frac{9}{4}$，
由x2+x≥$-\frac{1}{4}$得：当x2+x=$-\frac{1}{4}$，即x=-$\frac{1}{2}$时，函数取最小值-$\frac{11}{16}$，
故答案为：-$\frac{11}{16}$．
点评 本题考查的知识点是二次函数的图象和性质，函数的对称性，函数的零点，函数的最值，难度中档．
练习册系列答案
相关题目
7．
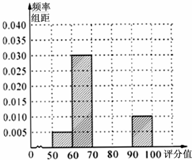某单位进行了主题为“你幸福吗”的幸福指数问卷调查，得到每个调查对象的幸福指数评分值（百分制）．现从收到的调查表中随机抽取20份进行统计，得到如图所示的频率分布表和频率分布直方图．
（Ⅰ）请完成题目中的频率分布表，并补全题目中的频率分布直方图；
（Ⅱ）该单位将随机邀请被问卷调查的部分员工参加“幸福教育”的座谈会．在抽样统计的这20人中，已知幸福指数评分值在区间（80，100]的5人中有2人被邀请参加座谈，求其中幸福指数评分值在区间（80，90]的仅有1人被邀请的概率．
某单位进行了主题为“你幸福吗”的幸福指数问卷调查，得到每个调查对象的幸福指数评分值（百分制）．现从收到的调查表中随机抽取20份进行统计，得到如图所示的频率分布表和频率分布直方图．（Ⅰ）请完成题目中的频率分布表，并补全题目中的频率分布直方图；
（Ⅱ）该单位将随机邀请被问卷调查的部分员工参加“幸福教育”的座谈会．在抽样统计的这20人中，已知幸福指数评分值在区间（80，100]的5人中有2人被邀请参加座谈，求其中幸福指数评分值在区间（80，90]的仅有1人被邀请的概率．
| 幸福指数评分值 | 频数 | 频率 |
| [50，60] | ||
| （60，70] | ||
| （70，80] | ||
| （80，90] | 3 | |
| （90，100] | ||
| 合 计 | 20 | 1 |
8．抛掷两枚质地均匀的骰子，向上的点数之和为7的概率是（ ）
| A． | $\frac{1}{9}$ | B． | $\frac{1}{6}$ | C． | $\frac{1}{18}$ | D． | $\frac{1}{12}$ |
9．定义行列式运算$|{\begin{array}{l}{a_1}&{a_2}\\{{a_3}}&{a_4}\end{array}}|$=a1a4-a2a3．将函数f（x）=$|{\begin{array}{l}{sin2x}&{\sqrt{3}}\\{cos2x}&1\end{array}}|$的图象向右平移$\frac{π}{6}$个单位后，所得函数图象的一个对称轴是（ ）
| A． | x=$\frac{7π}{12}$ | B． | x=$\frac{π}{2}$ | C． | x=$\frac{5π}{12}$ | D． | $x=\frac{π}{3}$ |