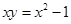题目内容
在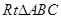 中 ,
中 ,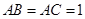 ,以点
,以点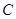 为一个焦点作一个椭圆,使这个椭圆
为一个焦点作一个椭圆,使这个椭圆
的另一焦点在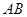 边上,且这个椭圆过
边上,且这个椭圆过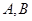 两点,则这个椭圆的焦距长为 .
两点,则这个椭圆的焦距长为 .
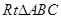 中 ,
中 ,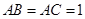 ,以点
,以点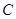 为一个焦点作一个椭圆,使这个椭圆
为一个焦点作一个椭圆,使这个椭圆的另一焦点在
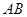 边上,且这个椭圆过
边上,且这个椭圆过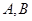 两点,则这个椭圆的焦距长为 .
两点,则这个椭圆的焦距长为 .
试题分析:因为题意中,在
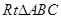 中 ,
中 ,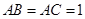 ,以点
,以点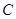 为一个焦点作一个椭圆,使这个椭圆的另一焦点在
为一个焦点作一个椭圆,使这个椭圆的另一焦点在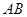 边上,且这个椭圆过
边上,且这个椭圆过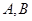 两点,设另一个焦点为D,则设BD=X,因为AD=1-X,在三角形ACD中,则AC+CD=2A=BC+BD,可得2-x=x+
两点,设另一个焦点为D,则设BD=X,因为AD=1-X,在三角形ACD中,则AC+CD=2A=BC+BD,可得2-x=x+ ,x=
,x= .在三角形CAD中,则1+(1-x)2=(2c)2,那么可知焦距的长为
.在三角形CAD中,则1+(1-x)2=(2c)2,那么可知焦距的长为
点评:关键是理解题意,根据题意能绘出图形,然后根据椭圆的定义,以及直角三角形的边长的关系来得到焦距,属于中档题 。

练习册系列答案
相关题目
 中,椭圆
中,椭圆 的焦距为2,且过点
的焦距为2,且过点 .
.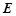 的方程;
的方程; ,
,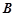 分别是椭圆
分别是椭圆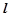 经过点
经过点 轴,点
轴,点 是椭圆上异于
是椭圆上异于 交
交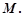

 的斜率为
的斜率为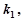 直线
直线 的斜率为
的斜率为 ,求证:
,求证: 为定值;
为定值; 垂直于
垂直于 的直线为
的直线为 .求证:直线
.求证:直线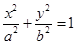 (a,b>0)过M(2,
(a,b>0)过M(2, ) ,N(
) ,N( ,1)两点,O为坐标原点.
,1)两点,O为坐标原点. ?若存在,写出该圆的方程,若不存在说明理由。
?若存在,写出该圆的方程,若不存在说明理由。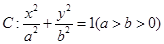 的离心率为
的离心率为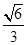 ,短轴一个端点到右焦点的距离为
,短轴一个端点到右焦点的距离为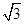 .
.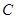 的方程;
的方程;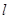 与椭圆
与椭圆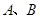 两点,坐标原点
两点,坐标原点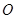 到直线
到直线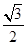 ,求
,求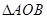

 与
与 轴交于点
轴交于点 ,与直线
,与直线
 交于点
交于点 ,椭圆
,椭圆 以
以 为右焦点,且过点
为右焦点,且过点 时,椭圆
时,椭圆



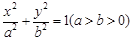 的右焦点为
的右焦点为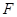 ,
,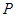 点在椭圆上,以
点在椭圆上,以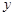 轴相切,且同时与
轴相切,且同时与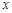 轴相切于椭圆的右焦点
轴相切于椭圆的右焦点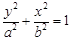 的离心率为 .
的离心率为 .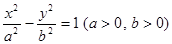 的左焦点
的左焦点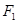 作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若
作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若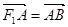 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )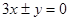 B.
B.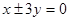
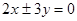 D.
D.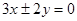
 的焦点与双曲线
的焦点与双曲线 的右焦点重合.
的右焦点重合. 的坐标分别是
的坐标分别是 ,直线
,直线 相交于点
相交于点 ,且直线
,且直线 与直线
与直线 的斜率之差是
的斜率之差是 ,则点
,则点