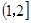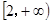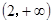题目内容
过双曲线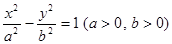 的左焦点
的左焦点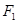 作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若
作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若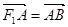 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A.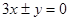 B.
B.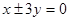
C.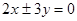 D.
D.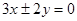
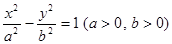 的左焦点
的左焦点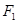 作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若
作斜率为1的直线,该直线与双曲线的两条渐近线的交点分别为A、B,若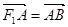 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )A.
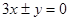 B.
B.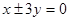
C.
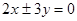 D.
D.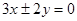
A
试题分析:双曲线的左焦点
 ,因而过左焦点
,因而过左焦点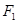 且斜率为1的直线
且斜率为1的直线 的方程为
的方程为 ,又双曲线的渐近线为
,又双曲线的渐近线为 ,所以由
,所以由 得,
得, ,则点A的纵坐标为
,则点A的纵坐标为 ,由
,由 得,
得, ,则点B的纵坐标为
,则点B的纵坐标为 ,另由
,另由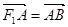 知,A为
知,A为 和B的中点,所以
和B的中点,所以 ,解得
,解得 ,所以双曲线的渐近线为
,所以双曲线的渐近线为 ,化为
,化为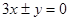 。故选A。
。故选A。点评:直线与曲线结合在一起的题目,一般都涉及到交点,而求交点需要联立方程组。

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
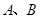 ,
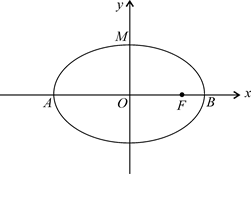
,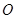 为椭圆中心,
为椭圆中心,
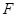 为椭圆的右焦点,
为椭圆的右焦点,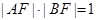 ,
,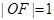 .
.
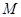 ,直线
,直线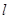 交椭圆于
交椭圆于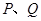 两点,问:是否存在直线
两点,问:是否存在直线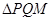 的垂心?若存在,求出直线
的垂心?若存在,求出直线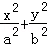 =1(a>b>0)的两个焦点分别为F1(﹣c,0),F2(c,0),M是椭圆短轴的一个端点,且满足
=1(a>b>0)的两个焦点分别为F1(﹣c,0),F2(c,0),M是椭圆短轴的一个端点,且满足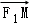
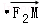 =0,点N( 0,3 )到椭圆上的点的最远距离为5
=0,点N( 0,3 )到椭圆上的点的最远距离为5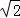
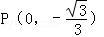 ;问A、B两点能否关于过点P、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
;问A、B两点能否关于过点P、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.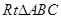 中 ,
中 ,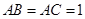 ,以点
,以点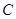 为一个焦点作一个椭圆,使这个椭圆
为一个焦点作一个椭圆,使这个椭圆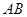 边上,且这个椭圆过
边上,且这个椭圆过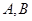 两点,则这个椭圆的焦距长为 .
两点,则这个椭圆的焦距长为 .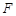 为抛物线
为抛物线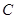 :
: 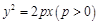 的焦点,
的焦点,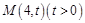 为抛物线
为抛物线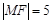 .
.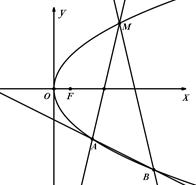
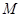 的坐标;
的坐标;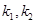 的两直线
的两直线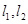 ,
, 与抛物线
与抛物线 ,
,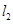 与抛物线
与抛物线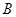 ,记直线
,记直线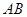 的斜率为
的斜率为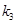 .
.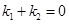 ,试求
,试求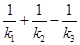 为定值.
为定值.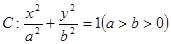 的两个焦点分别为
的两个焦点分别为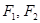 ,斜率为k的直线l过左焦点F1且与椭圆的交点为A,B与y轴交点为C,又B为线段CF1的中点,若
,斜率为k的直线l过左焦点F1且与椭圆的交点为A,B与y轴交点为C,又B为线段CF1的中点,若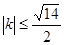 ,求椭圆离心率e的取值范围。
,求椭圆离心率e的取值范围。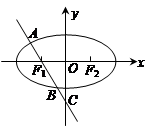
 ,过左焦点F1作斜率为
,过左焦点F1作斜率为 的直线交双曲线的右支于点P,且
的直线交双曲线的右支于点P,且 轴平分线段F1P,则双曲线的离心率是( )
轴平分线段F1P,则双曲线的离心率是( )



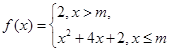 的图像与直线
的图像与直线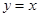 恰有三个公共点,则实数m的取值范围是( )
恰有三个公共点,则实数m的取值范围是( )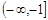
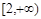
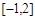
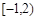
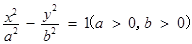 的右焦点是F, 过点F且倾角为600的直线与双曲线的右支有且只有一个交点,则此双曲线的离心率的范围是( )
的右焦点是F, 过点F且倾角为600的直线与双曲线的右支有且只有一个交点,则此双曲线的离心率的范围是( )