题目内容
9.过点M(5,$\frac{3}{2}$),且以直线y=±$\frac{1}{2}$x为渐近线的双曲线方程为$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{4}$=1.分析 依题意,可设所求的双曲线的方程为(x+2y)(x-2y)=λ,将点M(5,$\frac{3}{2}$)的坐标代入求得λ即可
解答 解:设所求的双曲线的方程为(x+2y)(x-2y)=λ,
∵点M(5,$\frac{3}{2}$)为该双曲线上的点,
∴λ=(5+3)(5-3)=16,
∴该双曲线的方程为:x2-4y2=16,即$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{4}$=1.
故答案为$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{4}$=1.
点评 本题考查双曲线的简单性质,着重考查待定系数法的应用,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.某几何体三视图如图所示,则该几何体的表面积为( )
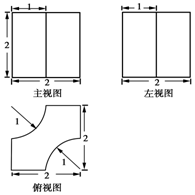

| A. | 8+2π | B. | 16+2π | C. | 20+2π | D. | 16+π |
14.在等差数列{an}中,a3+a6=11,a5+a8=39,则公差d为( )
| A. | -14 | B. | -7 | C. | 7 | D. | 14 |
4.下列说法正确的是( )
①|$\sqrt{(x+4)^{2}+{y}^{2}}$|-|$\sqrt{(x-4)^{2}+{y}^{2}}$=0
②|$\sqrt{(x+4)^{2}+{y}^{2}}$+$\sqrt{(x-4)^{2}+{y}^{2}}$=14
③|$\sqrt{(x+4)^{2}+{y}^{2}}$-$\sqrt{(x-4)^{2}+{y}^{2}}$|=6
④|$\sqrt{(x+4)^{2}+{y}^{2}}$-$\sqrt{(x-4)^{2}+{y}^{2}}$|=18.
①|$\sqrt{(x+4)^{2}+{y}^{2}}$|-|$\sqrt{(x-4)^{2}+{y}^{2}}$=0
②|$\sqrt{(x+4)^{2}+{y}^{2}}$+$\sqrt{(x-4)^{2}+{y}^{2}}$=14
③|$\sqrt{(x+4)^{2}+{y}^{2}}$-$\sqrt{(x-4)^{2}+{y}^{2}}$|=6
④|$\sqrt{(x+4)^{2}+{y}^{2}}$-$\sqrt{(x-4)^{2}+{y}^{2}}$|=18.
| A. | ①表示无轨迹 ②的轨迹是射线 | B. | ②的轨迹是椭圆 ③的轨迹是双曲线 | ||
| C. | ①的轨迹是射线④的轨迹是直线 | D. | ②、④均表示无轨迹 |
1.直线y=kx-3与圆(x-3)2+(y-2)2=4相交于M,N两点,若|MN|≥2$\sqrt{3}$,则k的取值范围是( )
| A. | [-$\frac{3}{4}$,0] | B. | (-∞,-$\frac{3}{4}$]∪[0,+∞) | C. | [-$\frac{\sqrt{3}}{3}$,$\frac{\sqrt{3}}{3}$] | D. | (-∞,-$\frac{\sqrt{3}}{3}$]∪[$\frac{\sqrt{3}}{3}$,+∞) |
 从椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上一点P向x轴作垂线,垂足恰为右焦点F2,A是椭圆与x轴负半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP,|F1A|=$\sqrt{10}$-$\sqrt{5}$,
从椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上一点P向x轴作垂线,垂足恰为右焦点F2,A是椭圆与x轴负半轴的交点,B是椭圆与y轴正半轴的交点,且AB∥OP,|F1A|=$\sqrt{10}$-$\sqrt{5}$,