题目内容
若关于x的方程f(x)=e|x|+|x|=k.有两个不同的实根,则实数k的取值范围是( )
| A、(0,1) |
| B、(1,+∞) |
| C、(-1,0) |
| D、(-∞,-1) |
考点:函数的零点与方程根的关系
专题:函数的性质及应用
分析:把方程e|x|=k-|x|恰有两个不同的实根,转化为一个函数y=e|x|的图象与一条折线y=k-|x|的位置关系研究,从而得出结论.
解答:
 解:方程f(x)=k化为:方程e|x|=k-|x|
解:方程f(x)=k化为:方程e|x|=k-|x|
令 y=e|x|,y=k-|x|,
y=k-|x|表示过斜率为1或-1的平行折线系,
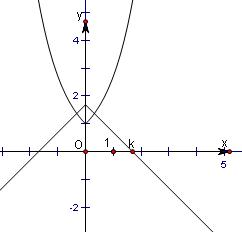
折线与曲线y=e|x|恰好有一个公共点时,有k=1,如图所示,
若关于x的方程f(x)=k有两个不同的实根,则实数k的取值范围是(1,+∞).
故选:B.
 解:方程f(x)=k化为:方程e|x|=k-|x|
解:方程f(x)=k化为:方程e|x|=k-|x|令 y=e|x|,y=k-|x|,
y=k-|x|表示过斜率为1或-1的平行折线系,
折线与曲线y=e|x|恰好有一个公共点时,有k=1,如图所示,
若关于x的方程f(x)=k有两个不同的实根,则实数k的取值范围是(1,+∞).
故选:B.
点评:本题主要考查根的存在性及根的个数判断,解答关键是利用直线与曲线的位置关系,属于基础题.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
sin2cos3tan4的值为( )
| A、负数 | B、正数 | C、0 | D、不存在 |
将一个球的直径扩大2倍,则其体积扩大( )倍.
| A、2 | B、4 | C、8 | D、16 |
已知x<0,函数y=
+x( )
| 4 |
| x |
| A、有最小值-4 |
| B、有最大值-4 |
| C、有最小值4 |
| D、有最大值4 |
设集合A={x|-3≤2x-1≤3},集合B=(1,+∞),则A∩B=( )
| A、(1,2) |
| B、[1,2] |
| C、[1,2) |
| D、(1,2] |
