题目内容
设有函数组:
①f(x)=
,g(x)=x+1;
②f(x)=
•
,g(x)=
;
③f(x)=
,g(x)=|x-1|;
④f(x)=2x-1,g(t)=2t-1.
其中表示同一个函数的有( )
①f(x)=
| x2-1 |
| x-1 |
②f(x)=
| x+1 |
| x-1 |
| x2-1 |
③f(x)=
| x2-2x+1 |
④f(x)=2x-1,g(t)=2t-1.
其中表示同一个函数的有( )
| A、①② | B、②④ | C、①③ | D、③④ |
考点:判断两个函数是否为同一函数
专题:函数的性质及应用
分析:判断两个函数的定义域以及对应法则是否相同,即可得到结果.
解答:
解:在①中,f(x)的定义域为{x|x≠1},g(x)=x+1的定义域为R,故不是同一函数;
在②中,f(x)的定义域为[1,+∞),g(x)的定义域为(-∞,-1]∪[1,+∞),故不是同一函数;
③f(x)=
,g(x)=|x-1|;定义域与对应法则相同,是相同函数.
④f(x)=2x-1,g(t)=2t-1.定义域与对应法则相同,是相同函数.
③④是同一函数.
故选:D.
在②中,f(x)的定义域为[1,+∞),g(x)的定义域为(-∞,-1]∪[1,+∞),故不是同一函数;
③f(x)=
| x2-2x+1 |
④f(x)=2x-1,g(t)=2t-1.定义域与对应法则相同,是相同函数.
③④是同一函数.
故选:D.
点评:本题考查函数是否相同的判断方法,基本知识的考查.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
要得到y=3sin2x的图象,只需将y=3sin(2x+
)的图象( )
| π |
| 4 |
A、向右平移
| ||
B、向左平移
| ||
C、向左平移
| ||
D、向右平移
|
| 5i2014 |
| 2-i |
| A、-2+i | B、-2-i |
| C、-1-2i | D、-1+2i |
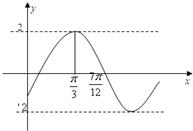 已知函数y=Asin(ωx+φ)(ω>0,A>0,|φ|<
已知函数y=Asin(ωx+φ)(ω>0,A>0,|φ|<| π |
| 2 |
A、y=sin(2x+
| ||
B、y=2sin(x-
| ||
C、y=2sin(2x-
| ||
D、y=2sin(2x+
|
定义在R上的函数f(x)的图象关于点(-
,0)成中心对称且对任意的实数x都有f(x)=-f(x+
)且f(-1)=1,f(0)=-2,则f(1)+f(2)+…+f(2014)=( )
| 3 |
| 4 |
| 3 |
| 2 |
| A、1 | B、0 | C、-1 | D、2 |
若|x|≤
,则函数f(x)=cos2x+sinx的最小值是( )
| π |
| 4 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
复数3i(3+4i)的虚部是( )
| A、9 | B、-12+9i |
| C、12 | D、9i |
直线2x-y+1=0与圆x2+y2-2mx-4my+m2-1=0的位置关系是( )
| A、相交但不过圆心 |
| B、相交且肯定过圆心 |
| C、相交或相切 |
| D、相交或相切或. |