题目内容

12．已知函数y=-|x-1|+2，画出函数的图象，确定函数的最值，并写出值域．

分析 化简y=-|x-1|+2=$\left\{\begin{array}{l}{-x+3，x≥1}\\{x+1，x＜1}\end{array}\right.$，作出函数的图象，从而写出函数的最值及值域即可．

解答 解：y=-|x-1|+2=$\left\{\begin{array}{l}{-x+3，x≥1}\\{x+1，x＜1}\end{array}\right.$，
作函数的图象如下，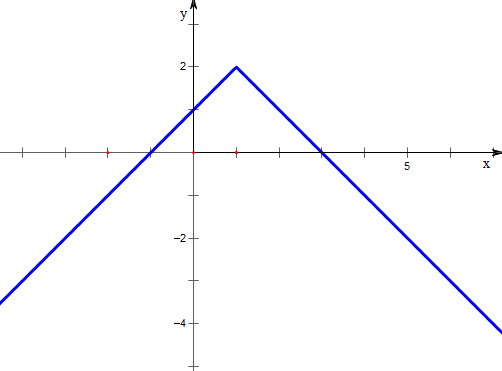

结合图象可知，
函数的最大值为2，没有最小值；
其值域为（-∞，2]．

点评 本题考查了函数的图象的作法及应用．

练习册系列答案
相关题目
2．比较大小：
（1）0.40.2，20.2，21.6；
（2）a-3，a3，b3，其中0＜a＜b＜1．
3．若函数f（x）=e${\;}^{-（x-m）^{2}}$（e为自然对数的底数）的最大值为m，则函数f（x）的单调递增区间是（-∞，1）．
20．已知函数f（x）=$\sqrt{{x}^{2}+x+m}$的定义域为R，求实数m的取值范围．
7．若曲线y=$\sqrt{9-{x}^{2}}$与直线y=2x+b始终有交点，则b的取值范围是（　　）
A．[-6，3$\sqrt{2}$]B．[-6，3$\sqrt{5}$]C．[-3$\sqrt{5}$，3$\sqrt{5}$]D．[-3$\sqrt{2}$，3$\sqrt{2}$]
17．1g2+1g100${\;}^{\frac{1}{2}-lg\sqrt{2}}$的值为（　　）
A．1B．2C．-1D．-2
4．求证：函数f（x）=1og2$\frac{x}{1-x}$在（0，1）上是增函数．
1．数列$\frac{1}{2×3}$，$\frac{-2}{3×4}$，$\frac{4}{4×5}$，$\frac{-8}{5×6}$，…，的一个通项公式是an=$\frac{（-1）^{n-1}{2}^{n-1}}{（n+1）（n+2）}$．
2．已知数列{an}为等差数列，首项a1=2，公差d=2，数列{bn}为等比数列，首项b1=3，公比为2．
（1）写出{an}，{bn}的通项公式；
（2）数列{cn}满足cn=anbn，求数列{cn}的前n项和Sn．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网