题目内容
一元二次不等式x2-bx-c＜0的解集是（-1，3 ），则b+c的值是（ ）
| A、-2 | B、2 | C、-5 | D、5 |
考点：一元二次不等式的解法
专题：不等式的解法及应用
分析：由不等式的解集得到不等式所对应的方程的根，在由根与系数关系列式求得b，c的值，则b+c可求．
解答：
解：∵一元二次不等式x2-bx-c＜0的解集是（-1，3 ），
∴-1，3是方程x2-bx-c=0的两根，
由根与系数关系得：
，
即b=2，c=3．
∴b+c=5．
故选：D．
∴-1，3是方程x2-bx-c=0的两根，
由根与系数关系得：
|
即b=2，c=3．
∴b+c=5．
故选：D．
点评：本题考查了一元二次不等式的解法，考查了一元二次方程根与系数关系，是基础的计算题．
练习册系列答案
相关题目
一个几何体的三视图如图所示，则该几何体的体积为（ ）
| A、2 | ||
| B、1 | ||
C、
| ||
D、
|
复数z=2-i（i为虚数单位）在复平面内对应的点所在象限为（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知全集U={1，2，3，4，5}，A={2，4，5}，则∁uA=（ ）
| A、∅ |
| B、{1，2，4} |
| C、{2，4，5} |
| D、{1，3} |
已知A（-2，0），B（2，0），点P在圆（x-3）2+（y-4）2=4上运动，则|PA|2+|PB|2的最小值是（ ）
| A、22 | B、10 | C、36 | D、26 |
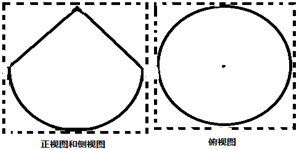如图实线所示，一个几何体的正视图和侧视图相同，俯视图为圆形，该几何体的三视图恰好可放在边长为2的正方形内（图中虚线所示），则该几何体的体积为（ ）A、1+
| ||
| B、2+π | ||
| C、π | ||
D、
|
若双曲线
-
=1的离心率为2，则实数m的值为（ ）
| x2 |
| 2 |
| y2 |
| m |
A、2
| ||
| B、3 | ||
C、
| ||
| D、6 |