题目内容
设函数 (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 (
(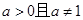 ).
).
(1)求 的值;
的值;
(2)求 在
在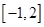 上的最大值;
上的最大值;
(3)当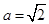 时,
时, 对所有的
对所有的 及
及 恒成立,求实数的取值范围.
恒成立,求实数的取值范围.
(1) ;(2)
;(2) ;(3)
;(3) 或
或 或
或 .
.
解析试题分析:(1)根据 为奇函数得到
为奇函数得到 ,恒有
,恒有 ,从而计算出
,从而计算出 的值;(2)根据指数函数的图像与性质对
的值;(2)根据指数函数的图像与性质对 进行分类讨论确定函数
进行分类讨论确定函数 的单调性,从而由单调性求出
的单调性,从而由单调性求出 在
在 的最大值;(3)先根据(2)计算出
的最大值;(3)先根据(2)计算出 ,然后将不等式的恒成立问题转化成
,然后将不等式的恒成立问题转化成 对
对 恒成立,接着构造关于
恒成立,接着构造关于 的函数
的函数 ,从而列出不等式组
,从而列出不等式组 ,求解不等式即可得出
,求解不等式即可得出 的取值范围.
的取值范围.
试题解析:(1)由 得
得  ,∴
,∴ 2分
2分
(2)∵ 3分
3分
①当 ,即
,即 时,
时, 在
在 上为增函数
上为增函数
 最大值为
最大值为 5分
5分
②当 ,即
,即 时,
时, 在
在 上为减函数
上为减函数 的最大值为
的最大值为 7分
7分 8分
8分
(3)由(2)得 在
在 上的最大值为
上的最大值为
 即
即 在
在 上恒成立 10分
上恒成立 10分
令
 即
即
所以 或
或 或
或 14分
14分
考点:1.一次与二次函数的图像与性质;2.指数函数的图像与性质;3.二次不等式.

练习册系列答案
相关题目
 ,
, .
. 在
在 上不具有单调性,求实数
上不具有单调性,求实数 的取值范围;
的取值范围;  .
. 的值;
的值; ,
, ,
, ,当
,当 时,试比较
时,试比较 ,
, ,
, 的大小.
的大小.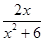 .
. 表示,且
表示,且 (其中
(其中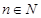 ),又知建5座球场时,每平方米的平均建筑费用为400元.
),又知建5座球场时,每平方米的平均建筑费用为400元.
 (
( 为常数),函数
为常数),函数 定义为:对每一个给定的实数
定义为:对每一个给定的实数 ,
,
 满足条件
满足条件 时,对于
时,对于 ,
,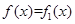 ;
; 是两个实数,满足
是两个实数,满足 ,且
,且 ,若
,若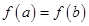 ,求函数
,求函数 上的单调递增区间的长度之和.(闭区间
上的单调递增区间的长度之和.(闭区间 的长度定义为
的长度定义为 )
)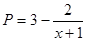 (其中
(其中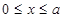 ,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为
,a为正常数);已知生产该产品还需投入成本(10+2P)万元(不含促销费用),产品的销售价格定为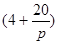 万元/万件.
万元/万件. ,
, .
. ;
;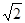 介于
介于 与
与 之间,且距
之间,且距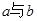 之间的距离是否可能为整数?若有,则求出这个整数;若没有,
之间的距离是否可能为整数?若有,则求出这个整数;若没有,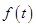 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)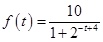 .(设该生物出生时t=0)
.(设该生物出生时t=0)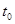 年,该生物长得最快,求
年,该生物长得最快,求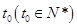 的值.
的值.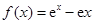 .
. 的最小值;
的最小值;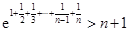
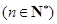 ;
; 与
与 定义域上的任意实数
定义域上的任意实数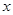 ,若存在常数
,若存在常数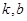 ,使得
,使得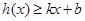 和
和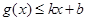 都成立,则称直线
都成立,则称直线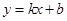 为函数
为函数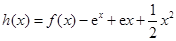 ,
,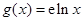 ,
,