题目内容
(14分)已知函数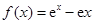 .
.
(Ⅰ)求函数 的最小值;
的最小值;
(Ⅱ)求证: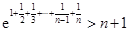
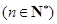 ;
;
(Ⅲ)对于函数 与
与 定义域上的任意实数
定义域上的任意实数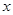 ,若存在常数
,若存在常数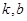 ,使得
,使得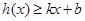 和
和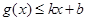 都成立,则称直线
都成立,则称直线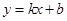 为函数
为函数 与
与 的“分界线”.设函数
的“分界线”.设函数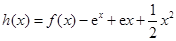 ,
,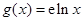 ,
, 与
与 是否存在“分界线”?若存在,求出
是否存在“分界线”?若存在,求出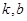 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(Ⅰ) 的最小值为
的最小值为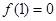 ;(Ⅱ)详见解析;(Ⅲ)
;(Ⅱ)详见解析;(Ⅲ)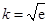 ,
,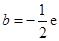
解析试题分析:(Ⅰ)求导得: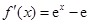 ,由此可得函数
,由此可得函数 在
在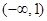 上递减,
上递减,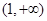 上递增,
上递增,
从而得 的最小值为
的最小值为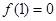 .
.
(Ⅱ)注意用第(Ⅰ)小题的结果.由(Ⅰ)知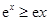 .这个不等式如何用?结合所在证的不等式可以看出,可以两端同时乘以
.这个不等式如何用?结合所在证的不等式可以看出,可以两端同时乘以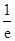 变形为:
变形为: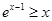 ,把
,把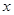 换成
换成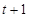 得
得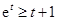 ,在这个不等式中令
,在这个不等式中令 然后将各不等式相乘即得.
然后将各不等式相乘即得.
(Ⅲ)结合题中定义可知,分界线就是一条把两个函数的图象分开的直线.那么如何确定两个函数是否存在分界线?显然,如果两个函数的图象没有公共点,则它们有无数条分界线,如果两个函数至少有两个公共点,则它们没有分界线.所以接下来我们就研究这两个函数是否有公共点.为此设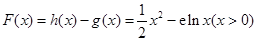 .通过求导可得当
.通过求导可得当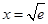 时
时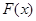 取得最小值0,这说明
取得最小值0,这说明 与
与 的图象在
的图象在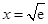 处有公共点
处有公共点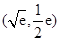 .如果它们存在分界线,则这条分界线必过该点.所以设
.如果它们存在分界线,则这条分界线必过该点.所以设 与
与 的“分界线”方程为
的“分界线”方程为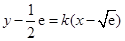 .由于
.由于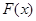 的最小值为0,所以
的最小值为0,所以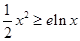 ,所以分界线必满足
,所以分界线必满足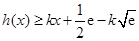 和
和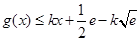 .下面就利用这两个不等式来确定
.下面就利用这两个不等式来确定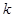 的值.
的值.
试题解析:(Ⅰ)解:因为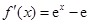 ,令
,令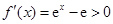 ,解得
,解得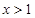 ,
,
令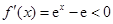 ,解得
,解得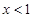 ,
,
所以函数 在
在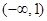 上递减,
上递减,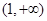 上递增,
上递增,
所以 的最小值为
的最小值为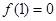 . 3分
. 3分
(Ⅱ)证明:由(Ⅰ)知函数 在
在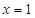 取得最小值,所以
取得最小值,所以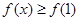 ,即
,即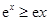
两端同时乘以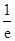 得
得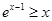 ,把
,把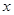 换成
换成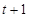 得
得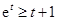 ,当且仅当
,当且仅当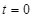 时等号成立.
时等号成立.
由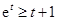 得,
得,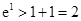 ,
,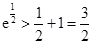 ,
, 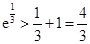 ,
, 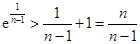 ,
,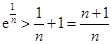 .
.
将上式相乘得 . 9分
. 9分
(Ⅲ)设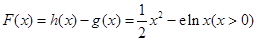 .
.
则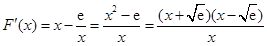 .
.
所以当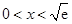 时,
时,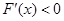 ;当
;当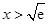 时,
时,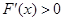 .
.
因此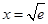 时
时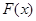 取得最小值0,则
取得最小值0,则 与
与 的图象在
的图象在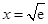 处有公共点
处有公共点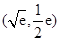 .
.
设 与
与 存在 “分界线”,方程为
存在 “分界线”,方程为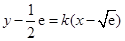 .
.
由

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
 (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 (
(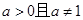 ).
). 在
在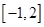 上的最大值;
上的最大值;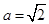 时,
时, 对所有的
对所有的 及
及 恒成立,求实数的取值范围.
恒成立,求实数的取值范围.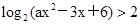 的解集是
的解集是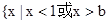 .
.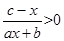 (c为常数) .
(c为常数) . 元.公司拟投入
元.公司拟投入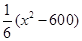 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入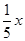 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价. (单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当
(单位:辆/千米)的函数.当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当 时,车流速度
时,车流速度 是车流密度x的一次函数.
是车流密度x的一次函数. 时,求函数
时,求函数 的表达式;
的表达式; 为多大时,车流量(单位时间内通过桥上某观察点的车辆数,单位:辆/每小时)
为多大时,车流量(单位时间内通过桥上某观察点的车辆数,单位:辆/每小时) 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时).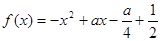 ,
, ,
, 的最大值
的最大值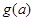 ;
; 吨,此时所需生产费用为(
吨,此时所需生产费用为(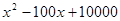 )万元,当出售这种商品时,每吨价格为
)万元,当出售这种商品时,每吨价格为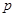 万元,这里
万元,这里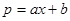 (
( 为常数,
为常数,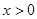 )
)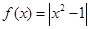 ,
,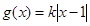 .
.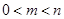 ,若
,若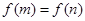 ,求
,求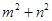 的值;
的值; ,当
,当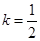 时,求
时,求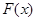 在
在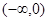 上的最小值;
上的最小值;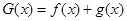 在区间
在区间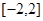 上的最大值.
上的最大值.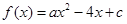 ,且
,且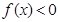 的解集是(1,5).
的解集是(1,5). 在
在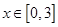 上的值域.
上的值域.