题目内容
某种海洋生物身体的长度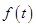 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)
满足如下的函数关系: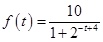 .(设该生物出生时t=0)
.(设该生物出生时t=0)
(1)需经过多少时间,该生物的身长超过8米;
(2)设出生后第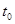 年,该生物长得最快,求
年,该生物长得最快,求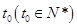 的值.
的值.
(1)6年;(2)4或5.
解析试题分析:(1)求需经过多少时间,该生物的身长超过8米,实质就是解不等式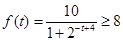 ,不等式解集中的最小值就是本题结论;(2)首先要搞懂什么是“长得最快”,“长得最快”就是说明这一年该生物身体增长的长度最大,因此实质就是求
,不等式解集中的最小值就是本题结论;(2)首先要搞懂什么是“长得最快”,“长得最快”就是说明这一年该生物身体增长的长度最大,因此实质就是求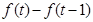 的最大值,即
的最大值,即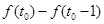 就是这个最大值,下面我们只要求出
就是这个最大值,下面我们只要求出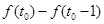 ,分析它的最大值是在
,分析它的最大值是在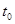 为何值时取得,
为何值时取得,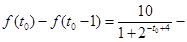
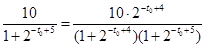 ,此式较繁,因此我们用换元法,设
,此式较繁,因此我们用换元法,设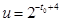 ,由有
,由有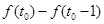
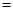
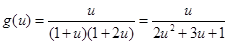 ,它的最大值求法一般是分子分母同时除以
,它的最大值求法一般是分子分母同时除以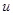 ,然后用基本不等式及不等式的性质得到结论.
,然后用基本不等式及不等式的性质得到结论.
试题解析:(1)设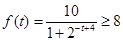 ,即
,即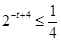 ,解得
,解得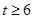 ,
,
即该生物6年后身长可超过8米; 5分
(2)设第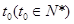 年生长最快,于是有
年生长最快,于是有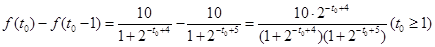 , 8分
, 8分
令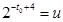 ,则
,则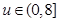 ,
,
令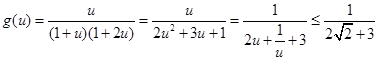 , 11分
, 11分
等号当且仅当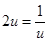 即
即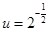 ,
, ,
,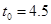 时成立,因为
时成立,因为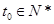 ,因此
,因此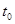 可能值为4或5,由
可能值为4或5,由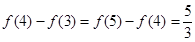 知,所求有年份为第4年和第5年,两年内各生长了
知,所求有年份为第4年和第5年,两年内各生长了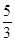 米. 14分
米. 14分
考点:(1)解不等式;(2)换元法与函数的最值.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
 (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 (
(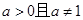 ).
). 在
在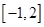 上的最大值;
上的最大值;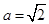 时,
时, 对所有的
对所有的 及
及 恒成立,求实数的取值范围.
恒成立,求实数的取值范围.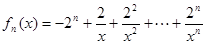 .
.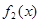 在
在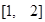 上的值域;
上的值域;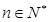 ,在
,在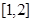 上存在唯一的
上存在唯一的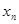 ,使得
,使得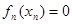 ;
; 的值.
的值.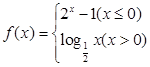 ,如果
,如果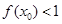 ,求
,求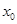 的取值范围.
的取值范围.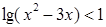
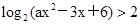 的解集是
的解集是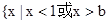 .
.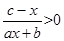 (c为常数) .
(c为常数) . 元.公司拟投入
元.公司拟投入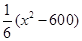 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入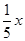 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.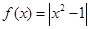 ,
,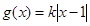 .
.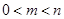 ,若
,若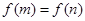 ,求
,求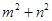 的值;
的值; ,当
,当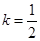 时,求
时,求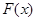 在
在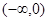 上的最小值;
上的最小值;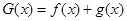 在区间
在区间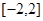 上的最大值.
上的最大值.