题目内容
已知函数 ,
, .
.
(1)若函数 在
在 上不具有单调性,求实数
上不具有单调性,求实数 的取值范围;
的取值范围;
(2)若 .
.
(ⅰ)求实数 的值;
的值;
(ⅱ)设 ,
, ,
, ,当
,当 时,试比较
时,试比较 ,
, ,
, 的大小.
的大小.
(1) (2)(ⅰ)2(ⅱ)
(2)(ⅰ)2(ⅱ)
解析试题分析:将二次函数 的解析式进行配方,根据其开口方向的对称轴得到该函数的单调区间, 函数
的解析式进行配方,根据其开口方向的对称轴得到该函数的单调区间, 函数 在
在 上不具有单调性,说明二次函数的对称轴在区间
上不具有单调性,说明二次函数的对称轴在区间 内,由此便可求出的取值范围;
内,由此便可求出的取值范围;
(2)(ⅰ)由 建立方程可解实数
建立方程可解实数 的值;
的值;
(ⅱ)分别根据二次函数、对数函数、指数函数的性质求出当 时,
时, ,
, ,
, 各自的取值范围,进而比较它们的大小.
各自的取值范围,进而比较它们的大小.
试题解析:解:(1)∵抛物线 开口向上,对称轴为
开口向上,对称轴为 ,
,
∴函数 在
在 单调递减,在
单调递减,在 单调递增, 2分
单调递增, 2分
∵函数 在
在 上不单调
上不单调
∴ ,得
,得 ,
,
∴实数 的取值范围为
的取值范围为 5分
5分
(2)(ⅰ)∵ ,
,
∴
∴实数 的值为
的值为 . 8分
. 8分
(ⅱ)∵ , 9分
, 9分 ,
, ,
,
∴当 时,
时, ,
, ,
, , 12分
, 12分
∴ . 13分
. 13分
考点:二次函数、指数函数、对数函数的性质.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
 t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N). ,证明数列{an}成等比数列,并求数列{xn}的通项公式.
,证明数列{an}成等比数列,并求数列{xn}的通项公式.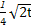 ,Q=
,Q= t,今该公司将5亿元投资于这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).求:
t,今该公司将5亿元投资于这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).求: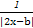 是偶函数,a为实常数.
是偶函数,a为实常数. x2+10x(万元);当年产量不小于80千件时,C(x)=51x+
x2+10x(万元);当年产量不小于80千件时,C(x)=51x+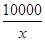 -1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1 450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完. (
( 为实常数)为奇函数,函数
为实常数)为奇函数,函数 (
(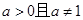 ).
). 在
在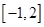 上的最大值;
上的最大值;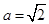 时,
时, 对所有的
对所有的 及
及 恒成立,求实数的取值范围.
恒成立,求实数的取值范围.