题目内容
15.已知实数x,y满足$\left\{\begin{array}{l}{2x-y+4≥0}\\{x+y-4≤0}\\{y≥0}\end{array}\right.$,则z=|x|-y的取值范围是( )| A. | [-2,4] | B. | [-2,2] | C. | [-4,4] | D. | [-4,2] |
分析 先画出满足条件的平面区域,通过讨论x的范围,求出直线的表达式,结合图象从而求出z的范围.
解答 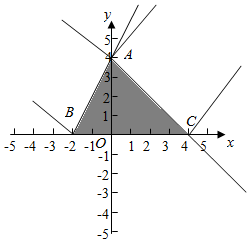 解:画出满足实数x,y满足$\left\{\begin{array}{l}{2x-y+4≥0}\\{x+y-4≤0}\\{y≥0}\end{array}\right.$的平面区域,如图示:A(0,4),B(-2,0),C(4,0).
解:画出满足实数x,y满足$\left\{\begin{array}{l}{2x-y+4≥0}\\{x+y-4≤0}\\{y≥0}\end{array}\right.$的平面区域,如图示:A(0,4),B(-2,0),C(4,0).
z=|x|-y=$\left\{\begin{array}{l}{x-y,x≥0}\\{-x-y,x<0}\end{array}\right.$,
当M(x,y)位于D中y轴的右侧包括y轴时,平移直线:x-y=0,可得x+y∈[-4,4],
当M(x,y)位于D中y轴左侧,平移直线-x-y=0,可得z=-x-y∈(2,4].
所以z=|x|-y的取值范围为:[-4,4].
故选:C.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
相关题目
6.已知tanθ=2,则$\frac{cosθ+sinθ}{cosθ-sinθ}$=( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | $\frac{2}{3}$ |
20.若双曲线$\frac{{x}^{2}}{8}$-y2=1的左焦点在抛物线y2=2px(p>0)的准线上,则p的值为( )
| A. | $\sqrt{7}$ | B. | 3 | C. | 2$\sqrt{7}$ | D. | 6 |
7.△ABC外接圆的半径为1,圆心为O,且2$\overrightarrow{OC}$+$\overrightarrow{CB}$+$\overrightarrow{CA}$=0,|$\overrightarrow{OC}$|=|$\overrightarrow{CB}$|,则$\overrightarrow{AC}$•$\overrightarrow{AB}$等于( )
| A. | $\frac{3}{2}$ | B. | $\sqrt{3}$ | C. | 3 | D. | 2$\sqrt{3}$ |
4.两灯塔A,B与海洋观察站C的距离都为a,灯塔A在C的北偏东30°,B在C的南偏东60°,则A,B两灯塔之间距离为( )
| A. | 2a | B. | $\sqrt{3}$a | C. | $\sqrt{2}$a | D. | a |