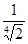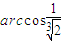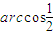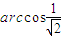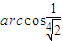题目内容
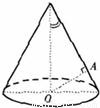
如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角的余弦值为( )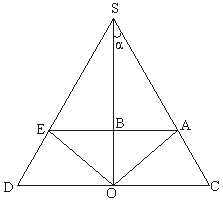
A.![]()
B.![]()
C.![]()
D.![]()
D
解:作圆锥的轴截面如图,在轴截面△SCD中,过A作AB⊥SO分别交SO、SD于B、E,连OE.因为OA绕轴SO旋转一周所得曲面将圆锥S-COD分成两部分,其上部分为两个同底的圆锥S-ABE和O-ABE的组合体.设圆锥S-COD、圆锥O-ABE、圆锥O-ABE的体积分别为V、V1、V2,OC=R,AB=r,SO=h

依题意得:V=2(V1+V2)
即![]()
![]() R2h=2(
R2h=2(![]()
![]() r2·SB+
r2·SB+![]()
![]() r2·BO)=
r2·BO)=![]()
![]() r2h,
r2h,
∴r=![]() R
R
又∵OA⊥SC,AB⊥SO,CO⊥SO,AB∥OC,
∴∠BAO=∠AOC=∠OSC=a
∴![]() =cos
=cos![]() =
=![]() ,
,
∴OA2=AB·OC=![]() R2
R2
∴OA=![]() R,
R,
∴cos![]() =
=![]() =
=![]()
∴选D

练习册系列答案
相关题目
 如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角的余弦值为( )
如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角的余弦值为( )A、
| |||||
B、
| |||||
C、
| |||||
D、
|
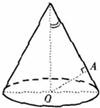 如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角为( )
如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角为( )A、arccos
| |||||
B、arccos
| |||||
C、arccos
| |||||
D、arccos
|

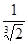 B.
B. C.
C.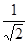 D.
D.