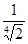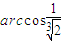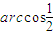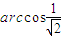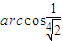题目内容
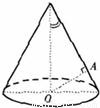
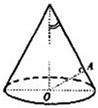 如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角的余弦值为( )
如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角的余弦值为( )A、
| |||||
B、
| |||||
C、
| |||||
D、
|
分析:设OB=1,求出OD,AC,利用OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,求得关系式,从而求得答案.
解答: 解:如图,设OB=1,则OD=ctgθ,AC=AD•sinθ,OD•cosθsinθ=cos2θ,
解:如图,设OB=1,则OD=ctgθ,AC=AD•sinθ,OD•cosθsinθ=cos2θ,
V圆锥DBB′=
ctgθ,V圆锥OAA′=
DO•πAC2=
ctgθ•πcos4θ,
由题意知cos4θ=
,故知cosθ=
.
故选D.
 解:如图,设OB=1,则OD=ctgθ,AC=AD•sinθ,OD•cosθsinθ=cos2θ,
解:如图,设OB=1,则OD=ctgθ,AC=AD•sinθ,OD•cosθsinθ=cos2θ,V圆锥DBB′=
| π |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
由题意知cos4θ=
| 1 |
| 2 |
| 1 | |||
|
故选D.
点评:本题考查旋转体的体积,三角函数等有关知识,是中档题.

练习册系列答案
相关题目
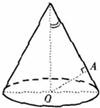 如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角为( )
如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分,则母线与轴的夹角为( )A、arccos
| |||||
B、arccos
| |||||
C、arccos
| |||||
D、arccos
|

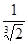 B.
B. C.
C.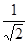 D.
D.