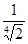题目内容
如图，OA是圆锥底面中心O到母线的垂线，OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分，则母线与轴的夹角为（ ）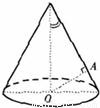
A．
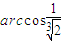
B．
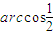
C．
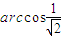
D．
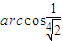
【答案】分析：设过A点的一条母线为BC，其中B为顶点，过A点作OB的垂线交OB于D，令圆锥体的体积为V，OC=R，DA=r，母线与轴夹角为∠OBA=∠β，求出上部两个圆锥的体积的和，再求出大圆锥的体积，两个之比为
，然后求出β的值．
解答：
解；设过A点的一条母线为BC，其中B为顶点，过A点作OB的垂线交OB于D，
令圆锥的体积为V，OC=R，DA=r，母线与轴夹角为∠OBO=∠β
将OBA看作是底面积相等的两个锥形，
r2π•BD+
r2π•0D=
V
r2π•OB=
V…①
V=
R2π•OB…②
由①、②得
R2=2•r2（R=r
），r=OA•COSβ
OA=R•COSβ，r=R•COS2β，COS2β=
=
β=
故选D．
点评：本题考查圆锥的结构特征，考查分析问题解决问题的能力，是基础题．
，然后求出β的值．解答：
解；设过A点的一条母线为BC，其中B为顶点，过A点作OB的垂线交OB于D，令圆锥的体积为V，OC=R，DA=r，母线与轴夹角为∠OBO=∠β
将OBA看作是底面积相等的两个锥形，
r2π•BD+r2π•0D=Vr2π•OB=V…①V=
R2π•OB…②由①、②得
R2=2•r2（R=r
），r=OA•COSβOA=R•COSβ，r=R•COS2β，COS2β=
=β=
故选D．
点评：本题考查圆锥的结构特征，考查分析问题解决问题的能力，是基础题．
练习册系列答案
相关题目
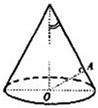如图，OA是圆锥底面中心O到母线的垂线，OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分，则母线与轴的夹角的余弦值为（ ）A、
| |||||
B、
| |||||
C、
| |||||
D、
|
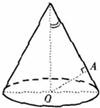如图，OA是圆锥底面中心O到母线的垂线，OA绕轴旋转一周所得曲面将圆锥分成体积相等的两部分，则母线与轴的夹角为（ ）A、arccos
| |||||
B、arccos
| |||||
C、arccos
| |||||
D、arccos
|
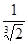B．
C．
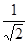D．
