题目内容
7.定义“等和数列”:在一个数列,如果每一项与它的后一项的和都为同一个常数,那么这个数列叫做等和数列,这个常数叫做该数列的公和.已知数列{an}是等和数,且a1=2,公和为5,则数列{an}的前n项和Sn=$\left\{\begin{array}{l}{\frac{5n}{2},n为偶数}\\{\frac{5n-1}{2},n为奇数}\end{array}\right.$.分析 由数列{an}是等和数,且a1=2,公和为5,可得5=a1+a2,解得a2=3.对n分类讨论即可得出.
解答 解:由数列{an}是等和数,且a1=2,公和为5,
∴5=a1+a2=2+a2,解得a2=3.
当n=2k(k∈N*)时,数列{an}的前n项和Sn=(a1+a2)+(a3+a4)+…+(a2k-1+a2k)=5+5+…+5=5k=$\frac{5n}{2}$.
当n=2k(k∈N*)时,数列{an}的前n项和Sn=(a1+a2)+(a3+a4)+…+(a2k-3+a2k-2)+a2k-1=$\frac{5(n-1)}{2}$+2=$\frac{5n-1}{2}$.
∴Sn=$\left\{\begin{array}{l}{\frac{5n}{2},n为偶数}\\{\frac{5n-1}{2},n为奇数}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{\frac{5n}{2},n为偶数}\\{\frac{5n-1}{2},n为奇数}\end{array}\right.$.
点评 本题考查了新定义“等和数列”的性质、数列求和方法,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.函数f(x)=x2+2x-1在闭区间[m,1]上有最大值2,最小值为-2,则m的取值范围是( )
| A. | [-1,1] | B. | (-∞,-1] | C. | [-3,-1] | D. | [-3,0] |
2.“a2+b2=0”是“函数y=ax2+bx+c的图象关于原点中心对称“的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
2.下列求导运算正确的是( )
| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{x^2}$ | B. | (log3x)′=$\frac{1}{xln3}$ | C. | (5x)′=5xlog5e | D. | (x2cosx)′=2xsinx |
16.在△ABC中,$B=\frac{π}{4},AB=\sqrt{2},BC=3$,则sinC=( )
| A. | $\frac{{\sqrt{10}}}{10}$ | B. | $\frac{{\sqrt{10}}}{5}$ | C. | $\frac{{3\sqrt{10}}}{10}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
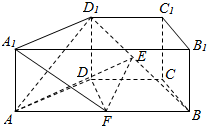 如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2DC=2,E为BD1的中点,F为AB的中点,∠DAB=60°.
如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是等腰梯形,AB∥CD,AB=2DC=2,E为BD1的中点,F为AB的中点,∠DAB=60°.