题目内容

2．“a2+b2=0”是“函数y=ax2+bx+c的图象关于原点中心对称“的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件

分析 由题意可知：“a2+b2=0”则a=b=0，只有当c=0时，若函数y=ax2+bx+c的图象关于原点中心对称，而图象关于原点对称a=c=0，由充要条件的定义可得．

解答 解：“a2+b2=0”，则a=b=0，则y=ax2+bx+c=c，该图象只有当c=0时，才关于原点对称，
若函数y=ax2+bx+c的图象关于原点中心对称，则a=0，c=0，
故“a2+b2=0”是“函数y=ax2+bx+c的图象关于原点中心对称“的既不充分也不必要条件，
故选：D．

点评 本题考查充要条件的判断，涉及二次函数的知识，属基础题．

练习册系列答案
相关题目
12．在0°～360°间，找出与下列各角终边相同的角，并判定它们是第几象限角：
（1）-150°；
（2）660°；
（3）950°12′．
13．已知函数y=$\frac{a{x}^{2}-8x+b}{{x}^{2}+1}$的值域是[1，9]，则a+b=10．
10．△ABC中若面积sinA•cosB-sinB=sinC-sinA•cosC且周长为12，则其面积最大值为108-72$\sqrt{2}$．
17．点A，B，C，D在格点图的位置如图所示，则向量$\overrightarrow{AD}$+$\overrightarrow{AC}$在$\overrightarrow{AB}$方向上的投影为（　　）
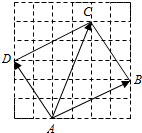
A．-$\frac{\sqrt{5}}{5}$B．-$\frac{8\sqrt{5}}{5}$C．$\frac{8\sqrt{5}}{5}$D．2
7．已知向量$\overrightarrow{m}$=（sinx，-1），$\overrightarrow{n}$=（cosx，$\frac{3}{2}$），f（x）=（$\overrightarrow{m}$+$\overrightarrow{n}$）•$\overrightarrow{m}$．
（1）求f（x）的最小正周期及单调递增区间；
（2）当x∈[0，$\frac{π}{2}$]时，求f（x）的值域；
（3）将f（x）的图象左移$\frac{3π}{8}$个单位后得g（x）的图象，求g（x）在[-$\frac{π}{3}$，$\frac{π}{3}$]上的最大值．
14．已知x-x-1=1，那么x3-x-3的值为 （　　）
A．1B．2C．3D．4
7．定义“等和数列”：在一个数列，如果每一项与它的后一项的和都为同一个常数，那么这个数列叫做等和数列，这个常数叫做该数列的公和．已知数列{an}是等和数，且a1=2，公和为5，则数列{an}的前n项和Sn=$\left\{\begin{array}{l}{\frac{5n}{2}，n为偶数}\\{\frac{5n-1}{2}，n为奇数}\end{array}\right.$．
8．已知集合P={x|x2+x-6=0}，S={x|ax+1=0}，且S⊆P
求：由a的可取值组合的集合．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网