题目内容

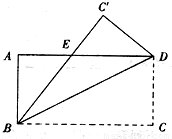
如图，把长方形ABCD沿BD对折，使C点落在C′的位置时，BC′与AD交于E，若AB=6cm，BC=8cm，求重叠部分△BED的面积．
分析：先判断三角形全等，再根据勾股定理求出AE长，利用矩形的面积减去两个小三角形的面积即可
解答：解：∵AB=DC′，∠AEB=∠DC′E，∠A=∠C′
∴△ABE≌△C′DE
∴BE=DE，设AE=x，则BE=DE=8-x
由勾股定理：62+x2=（8-x）2
解得 x=
7
4

∴S△BDE=6×8-2×
1
2
×AB×AE=48-6×
7
4
=37.5．
答：重叠部分面积为37.5cm2
点评：本题考查平面几何面积计算．
练习册系列答案
相关题目
（2013•揭阳二模）在图（1）所示的长方形ABCD中，AD=2AB=2，E、F分别为AD、BC的中点，M、N两点分别在AF和CE上运动，且AM=EN=a(0＜a＜
2
)．把长方形ABCD沿EF折成大小为θ的二面角A-EF-C，如图（2）所示，其中θ∈(0，
π
2
]
（1）当θ=45°时，求三棱柱BCF-ADE的体积；
（2）求证：不论θ怎么变化，直线MN总与平面BCF平行；
（3）当θ=900且a=
2
2
．时，求异面直线MN与AC所成角的余弦值．

如图，已知长方形ABCD中，AB＝2，A1，B1分别是AD，BC边上的点，且AA1=BB1="1," E，F分别为B1D与AB的中点. 把长方形ABCD沿直线折成直角二面角，且.

（1）求证：

（2）求三棱锥的体积.

 
在图（1）所示的长方形ABCD中，AD=2AB=2，E、F分别为AD、BC的中点，M、N两点分别在AF和CE上运动，且AM=EN=a(0＜a＜
2
)．把长方形ABCD沿EF折成大小为θ的二面角A-EF-C，如图（2）所示，其中θ∈(0，
π
2
]
精英家教网

（1）当θ=45°时，求三棱柱BCF-ADE的体积；
（2）求证：不论θ怎么变化，直线MN总与平面BCF平行；
（3）当θ=900且a=
2
2
．时，求异面直线MN与AC所成角的余弦值．
如图，把长方形ABCD沿BD对折，使C点落在C′的位置时，BC′与AD交于E，若AB=6cm，BC=8cm，求重叠部分△BED的面积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网