题目内容
(本小题满分12分)在三棱锥 中,
中, 。
。

(1)求证: ;
;
(2)求二面角 的余弦值的绝对值。
的余弦值的绝对值。
(1)详见解析;(2) .
.
【解析】
试题分析:(1)设 为
为 中点,连结
中点,连结 ,
, 利用等腰三角形的性质可证
利用等腰三角形的性质可证 ⊥平面
⊥平面 ,
,
从而证明 ⊥
⊥ ;
;
(2)如图,建立空间直角坐标系 .其中AB∥x轴,利用空间向量的坐标运算求出平面
.其中AB∥x轴,利用空间向量的坐标运算求出平面 的法向量
的法向量 和平面
和平面 的法向量
的法向量 ,进而利用向量的夹角公式求出二面角
,进而利用向量的夹角公式求出二面角 的余弦值的绝对值.
的余弦值的绝对值.
试题解析:【解析】
(1)设 为
为 中点,连结
中点,连结 ,
,
 ,
,  ,
,
 ⊥
⊥ ,
, .
.
同理,  ⊥
⊥ ,
,
∴ ⊥平面
⊥平面
所以 ⊥
⊥
(2)如图,建立空间直角坐标系 .其中AB∥x轴
.其中AB∥x轴
易得 ,又
,又



则 ,A
,A ,
, ,
, ,
,
 ,
, .
.
设平面 的法向量为
的法向量为 ,
,
则 .
.
 平面
平面 的一个法向量
的一个法向量 .
.
 ,
,
同理可求得平面CBP的一个法向量为
 .
.
考点:1、空间直线与平面的位置关系;2、空间向量在立体几何中的应用.

练习册系列答案
相关题目
 满足约束条件
满足约束条件 ,则目标函数
,则目标函数 的最小值为( )
的最小值为( ) B.
B. C.
C. D.
D.
 (C)
(C) (D)
(D)
 ,则它们的图象可能是( )
,则它们的图象可能是( )
 的最小正周期为
的最小正周期为 ,则
,则 ( )
( ) C.-1 D.
C.-1 D.
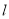 过椭圆
过椭圆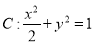 的左焦点
的左焦点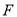 ,且与椭圆
,且与椭圆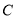 交于
交于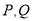 两点,
两点,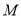 为弦
为弦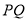 的中点,
的中点,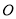 为原点,若
为原点,若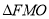 是以线段
是以线段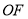 为底边的等腰三角形,则直线
为底边的等腰三角形,则直线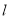 的斜率为
的斜率为  ,深
,深 的空穴,则取出该球前,球面上的点到冰面的最大距离为( )
的空穴,则取出该球前,球面上的点到冰面的最大距离为( ) B.
B. C.
C. D.
D.
 中,
中, ,则
,则 __________.
__________. 的最小正周期是 .
的最小正周期是 .