题目内容
直线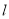 过椭圆
过椭圆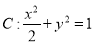 的左焦点
的左焦点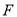 ,且与椭圆
,且与椭圆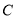 交于
交于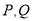 两点,
两点,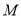 为弦
为弦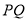 的中点,
的中点,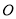 为原点,若
为原点,若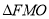 是以线段
是以线段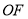 为底边的等腰三角形,则直线
为底边的等腰三角形,则直线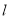 的斜率为
的斜率为

【解析】
试题分析:由椭圆的标准方程 得:
得: 所以其左焦点的坐标为
所以其左焦点的坐标为 ,设直线
,设直线 的斜率为
的斜率为 ,则直线
,则直线 的方程为:
的方程为:
联立方程组 ,消去
,消去 得:
得:
整理得: (*)
(*)
设 ,则是方关于
,则是方关于 的方程(*)的两根,
的方程(*)的两根,
所以,
由题设 是以线段
是以线段 为底边的等腰三角形,所以
为底边的等腰三角形,所以
所以, ,解得:
,解得: ,所以
,所以
所以答案应填: .
.
考点:直线与椭圆的位置关系.

练习册系列答案
相关题目
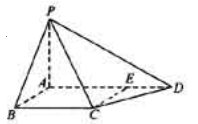
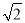 ,∠CDA=45°,求四棱锥P-ABCD的体积
,∠CDA=45°,求四棱锥P-ABCD的体积 的焦点
的焦点 的直线交抛物线于
的直线交抛物线于 两个不同的点,过
两个不同的点,过 分别作抛物线的切线,且二者相交于点
分别作抛物线的切线,且二者相交于点

 ;
; 的面积的最小值。
的面积的最小值。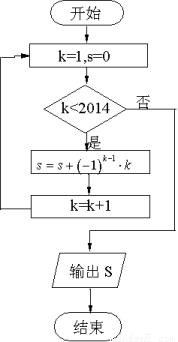
 中,
中, 。
。
 ;
; 的余弦值的绝对值。
的余弦值的绝对值。 ,则它们的图象可能是( )
,则它们的图象可能是( )
 的最小正周期为
的最小正周期为 ,则
,则 ( )
( ) C.-1 D.
C.-1 D.
 有唯一的零点,则实数
有唯一的零点,则实数 的值为( )
的值为( ) 的公比
的公比 ,
, ,
, ,则
,则 前5项和
前5项和 等于
等于 (B)
(B)
 (D)
(D)