题目内容
 如图,四棱锥P-ABCD中,侧面△ADE为等边三角形,底面BCDE是等腰梯形,且CD∥BE,DE=2,CD=4,∠CDE=60°,M为DE的中点,F为AC的中点,且AC=4.
如图,四棱锥P-ABCD中,侧面△ADE为等边三角形,底面BCDE是等腰梯形,且CD∥BE,DE=2,CD=4,∠CDE=60°,M为DE的中点,F为AC的中点,且AC=4.(1)求证:平面AED⊥平面BCD;
(2)求证:FB∥平面ADE;
(3)求四棱锥A-BCDE的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)首先根据直线与平面垂直的判定定理证明AM⊥平面BCD,然后根据平面垂直的判定定理证明平面ADE⊥平面BCD.
(2)取DC中点N,首先证明FN∥平面ADE,然后再证明BN∥平面ADE,再根据平面与平面平行的判定定理证明平面ADE∥平面FNB,最后由面面平行的性质证明FB∥平面ADE.
(3)由AM⊥平面BCD,AM=
,由此能求出四棱锥A-BCDE的体积.
(2)取DC中点N,首先证明FN∥平面ADE,然后再证明BN∥平面ADE,再根据平面与平面平行的判定定理证明平面ADE∥平面FNB,最后由面面平行的性质证明FB∥平面ADE.
(3)由AM⊥平面BCD,AM=
| 3 |
解答:
(1)证明:∵△ADE是等边三角形,DE=2,M是DE的中点,
∴AM⊥DE,AM=
,
∵底面BCDE是等腰梯形,
且CD∥BE,DE=2,CD=4,∠CDE=60°,
M为DE的中点,F为AC的中点,且AC=4
∴在△DMC中,DM=1,MC2=16+1-2×4×1×cos60°=13,
即MC=
,
在△AMC中,AM2+MC2=3+13=16=AC2,
∴AM⊥MC,
又AM⊥DE,MC∩DE=M,∴AM⊥平面BCD,
∵AM?平面ADE,∴平面ADE⊥平面BCD.
(2)证明:取DC的中点N,连结FN,NB,
∵F,N分别是AC,DC的中点,
∴FN∥AD,
∵FN不包含于平面ADE,AD?平面ADE,
∴FN∥平面ADE,
∵N是DC的中点,∴BC=NC=2,
又∠CDE=60°,∴△BCN是等边三角形,
∴BN∥DE,∵FN∩BN=N,∴平面ADE∥平面FNB,
∵FB⊆平面FNB,∴FB∥平面ADE.
(3)解:由(1)知AM⊥平面BCD,AM=
,
∵底面BCDE是等腰梯形,且CD∥BE,DE=2,CD=4,∠CDE=60°,
∴BE=4-1-1=2,等腰梯形BCDE的高为
,
∴四棱锥A-BCDE的体积:
V=
×S梯形BCDE×AM
=
×(4+2)×
×
=3.

∴AM⊥DE,AM=
| 3 |
∵底面BCDE是等腰梯形,
且CD∥BE,DE=2,CD=4,∠CDE=60°,
M为DE的中点,F为AC的中点,且AC=4
∴在△DMC中,DM=1,MC2=16+1-2×4×1×cos60°=13,
即MC=
| 13 |
在△AMC中,AM2+MC2=3+13=16=AC2,
∴AM⊥MC,
又AM⊥DE,MC∩DE=M,∴AM⊥平面BCD,
∵AM?平面ADE,∴平面ADE⊥平面BCD.
(2)证明:取DC的中点N,连结FN,NB,
∵F,N分别是AC,DC的中点,
∴FN∥AD,
∵FN不包含于平面ADE,AD?平面ADE,
∴FN∥平面ADE,
∵N是DC的中点,∴BC=NC=2,
又∠CDE=60°,∴△BCN是等边三角形,
∴BN∥DE,∵FN∩BN=N,∴平面ADE∥平面FNB,
∵FB⊆平面FNB,∴FB∥平面ADE.
(3)解:由(1)知AM⊥平面BCD,AM=
| 3 |
∵底面BCDE是等腰梯形,且CD∥BE,DE=2,CD=4,∠CDE=60°,
∴BE=4-1-1=2,等腰梯形BCDE的高为
| 3 |
∴四棱锥A-BCDE的体积:
V=
| 1 |
| 3 |
=
| 1 |
| 3 |
| ||
| 2 |
| 3 |
点评:本题考查平面与平面垂直的证明,考查直线与平面平行的证明,考查四棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

 一个圆锥的底面半径为2cm,高为6cm,在圆锥内部有一个高为xcm的内接圆柱.(如图为轴截面图)
一个圆锥的底面半径为2cm,高为6cm,在圆锥内部有一个高为xcm的内接圆柱.(如图为轴截面图)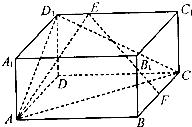 如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数).
如图,在长方体ABCD-A1B1C1D1中,AB=4,AD=2,AA1=2,F是棱BC的中点,点E在棱C1D1上,且D1E=λEC1(λ为实数).