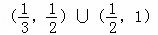题目内容
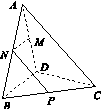
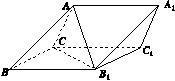
如图16所示,四棱柱ABCD A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求二面角C1OB1D的余弦值.
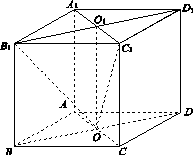
图16
解:(1)如图(a),因为四边形ACC1A1为矩形,所以CC1⊥AC.同理DD1⊥BD.
因为CC1∥DD1,所以CC1⊥BD.而AC∩BD=O,因此CC1⊥底面ABCD.
由题设知,O1O∥C1C.故O1O⊥底面ABCD.
(2)方法一: 如图(a),过O1作O1H⊥OB1于H,连接HC1.
由(1)知,O1O⊥底面ABCD,所以O1O⊥底面A1B1C1D1,于是O1O⊥A1C1.
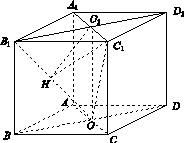
图(a)
又因为四棱柱ABCD A1B1C1D1的所有棱长都相等,所以四边形A1B1C1D1是菱形,
因此A1C1⊥B1D1,从而A1C1⊥平面BDD1B1,所以A1C1⊥OB1,于是OB1⊥平面O1HC1.
进而OB1⊥C1H.故∠C1HO1是二面角C1OB1D的平面角.
不妨设AB=2.因为∠CBA=60°,所以OB= ,OC=1,OB1=
,OC=1,OB1=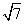 .
.
在Rt△OO1B1中,易知O1H=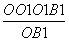 =2
=2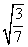 .而O1C1=1,于是C1H=
.而O1C1=1,于是C1H=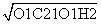 =
=
即二面角C1OB1D的余弦值为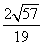 .
.
方法二:因为四棱柱ABCD A1B1C1D1的所有棱长都相等,所以四边形ABCD是菱形,因此AC⊥BD.又O1O⊥底面ABCD,从而OB,OC,OO1两两垂直.
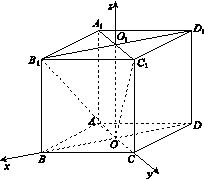
图(b)
如图(b),以O为坐标原点,OB,OC,OO1所在直线分别为x轴,y轴,z轴,建立空间直角坐标系O xyz,不妨设AB=2.因为∠CBA=60°,所以OB= ,OC=1,于是相关各点的坐标为O(0,0,0),
,OC=1,于是相关各点的坐标为O(0,0,0),
B1( ,0,2),C1(0,1,2).
,0,2),C1(0,1,2).
易知,n1=(0,1,0)是平面BDD1B1的一个法向量.
 故二面角C1OB1D的余弦值为
故二面角C1OB1D的余弦值为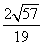 .
.

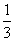 ,乙、丙去北京旅游的概率分别为
,乙、丙去北京旅游的概率分别为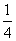 ,
,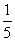 .假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为( )
.假定三人的行动相互之间没有影响,那么这段时间内至少有1人去北京旅游的概率为( ) B.
B.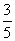
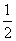 D.
D.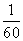
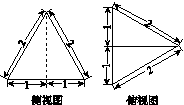
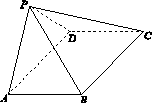
 ,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
,PC=2,问AB为何值时,四棱锥P ABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.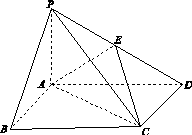
 ,n=1,2,3,…,10}中任取一个元素,所取元素恰好满足方程cosx=
,n=1,2,3,…,10}中任取一个元素,所取元素恰好满足方程cosx=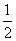 的概率是________.
的概率是________.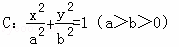 的左右焦点分别为F1,F2,若椭圆C上恰好有6个不同的点P,使得△F1F2P为等腰三角形,则椭圆C的离心率的取值范围是( )
的左右焦点分别为F1,F2,若椭圆C上恰好有6个不同的点P,使得△F1F2P为等腰三角形,则椭圆C的离心率的取值范围是( )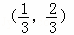 B.
B. 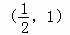 C.
C. 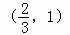 D.
D.