题目内容
已知数列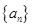 的前
的前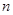 项和是
项和是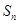 ,且
,且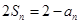 .求数列
.求数列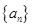 的通项公式;
的通项公式;
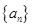 的前
的前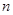 项和是
项和是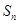 ,且
,且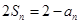 .求数列
.求数列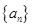 的通项公式;
的通项公式;
试题分析:由题意根据数列前
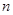 项和定义,尽可能对条件
项和定义,尽可能对条件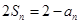 进行挖掘利用,因为
进行挖掘利用,因为 ,所以由条件可求出数列
,所以由条件可求出数列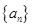 的首项
的首项 ,当
,当 时,有
时,有 ,由条件可得
,由条件可得 ,即
,即 ,从而发现数列
,从而发现数列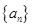 是以首项为
是以首项为 ,公比为
,公比为 的等比数列,再由等比数列的通项公式可求得数列
的等比数列,再由等比数列的通项公式可求得数列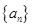 的通项公式.
的通项公式.试题解析:当
 时,
时, ,
, ,∴
,∴ ; 2分
; 2分当
 时,
时, 4分
4分两式相减得
 ,即
,即 ,又
,又 ,∴
,∴ 8分
8分∴数列
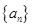 是以
是以 为首项,
为首项, 为公比的等比数列. 10分
为公比的等比数列. 10分∴
 12分
12分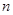 项和定义;2.等比数列.
项和定义;2.等比数列.
练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
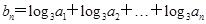 ,求数列
,求数列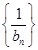 的前n项和.
的前n项和.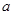 为实数,数列
为实数,数列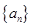 满足
满足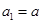 ,当
,当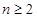 时,
时,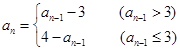 ,
, 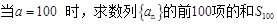 ;(5分)
;(5分)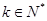 ,使
,使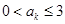 ;(5分)
;(5分)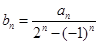 ,当
,当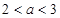 时,求证:
时,求证: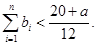 (6分)
(6分)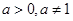 ,数列
,数列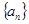 是首项为
是首项为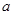 ,公比也为
,公比也为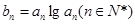
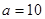 ,求数列
,求数列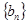 的前
的前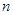 项和
项和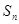 ;
;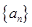 的前
的前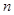 项和为
项和为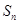 ,数列
,数列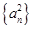 的前
的前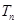 ,且
,且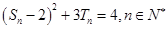 .
.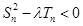 对
对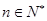 恒成立,求
恒成立,求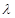 的最小值;
的最小值;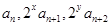 成等差数列,求正整数
成等差数列,求正整数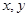 的值.
的值.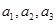 的和为定值
的和为定值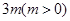 ,且公比为
,且公比为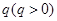 ,令
,令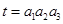 ,则
,则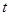 的取值范围为( )
的取值范围为( )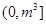
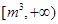
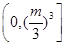
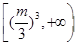
 }中,
}中, 则
则 ( )
( ) 

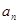 }的前n项和为
}的前n项和为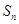 ,且
,且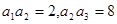 ,则
,则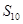 = __________.
= __________. 中,
中, ,
, ,则数列
,则数列 .
.