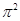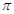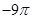题目内容
等比数列{an}的各项均为正数,且2a1+3a2=1,a32=9a2a6.
(1)求数列{an}的通项公式;
(2)设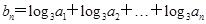 ,求数列
,求数列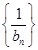 的前n项和.
的前n项和.
(1)求数列{an}的通项公式;
(2)设
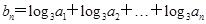 ,求数列
,求数列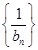 的前n项和.
的前n项和.(1) ;(2)
;(2)
 ;(2)
;(2)
试题分析:(1)由
 得
得 ,从而求
,从而求 ,再代入
,再代入 求
求 ,代入等比数列通项公式求
,代入等比数列通项公式求 ;(2)求数列前n项和,首先考察数列通项公式,根据通项公式的不同形式选择相应的求和方法,由
;(2)求数列前n项和,首先考察数列通项公式,根据通项公式的不同形式选择相应的求和方法,由 =
= ,故求得
,故求得
 ,利用裂项相消法求和.
,利用裂项相消法求和.试题解析:(1)设数列{an}的公比为q.由
 得
得 ,所以
,所以 .由条件可知
.由条件可知 故
故
由
 得
得 ,所以
,所以 .故数列{an}的通项公式为
.故数列{an}的通项公式为 .
.(2)
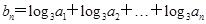

 .
.故


 .
.


所以数列
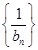 的前n项和为
的前n项和为 .
.
练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
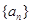 的前
的前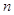 项和为
项和为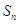 ,且
,且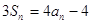 .
.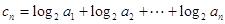 ,
,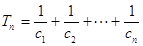 ,求使
,求使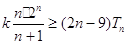 恒成立的实数
恒成立的实数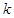 的取值范围.
的取值范围.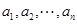 为
为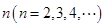 阶“期待数列”:
阶“期待数列”: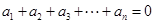 ;②
;②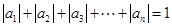 .
.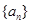 的通项公式是
的通项公式是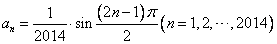 ,
,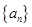 为
为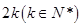 阶“期待数列”,求公比q及
阶“期待数列”,求公比q及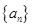 的前
的前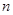 项和是
项和是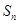 ,且
,且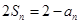 .求数列
.求数列 的等边三角形(图(1));二级分形图是将一级分形图的每条线段三等分,并以中间的那一条线段为一底边向形外作等边三角形,然后去掉底边(图(2));将二级分形图的每条线段三等边,重复上述的作图方法,得到三级分形图(图(3));…;重复上述作图方法,依次得到四级、五级、…、
的等边三角形(图(1));二级分形图是将一级分形图的每条线段三等分,并以中间的那一条线段为一底边向形外作等边三角形,然后去掉底边(图(2));将二级分形图的每条线段三等边,重复上述的作图方法,得到三级分形图(图(3));…;重复上述作图方法,依次得到四级、五级、…、 级分形图.则
级分形图.则
 中,已知对任意正整数
中,已知对任意正整数 ,
, ,则
,则 等于( )
等于( )



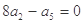 ,则
,则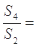 ( )
( )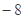
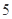
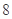
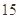
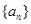 ,且
,且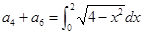 ,则
,则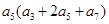 的值为( )
的值为( )