题目内容
16.已知点A(-1,3),F是抛物线x2=4y的焦点,M是抛物线上任意一点,则|MF|+|MA|的最小值为4;点M到直线x-y-2=0的距离的最小值为$\frac{{\sqrt{2}}}{2}$.分析 设点M在准线上的射影为D,则根据抛物线的定义可知|MF|=|MD|进而把问题转化为求|MA|+|MD|取得最小,进而可推断出当D,M,A三点共线时|MA|+|MD|最小,答案可得,利用点到直线的距离公式,结合配方法求出点M到直线x-y-2=0的距离的最小值
解答 解:设点M在准线上的射影为D,则根据抛物线的定义可知|MF|=|MD|,
∴要求|MA|+|MF|取得最小值,即求|MA|+|MD|取得最小,
当D,M,A三点共线时|MA|+|MD|最小,为3-(-1)=4.
点M到直线x-y-2=0的距离为$\frac{|x-y-2|}{\sqrt{2}}$=$\frac{|\frac{1}{4}(x-2)^{2}+1|}{\sqrt{2}}$,∴x=2时,取得最小值$\frac{{\sqrt{2}}}{2}$.
故答案为:4;$\frac{{\sqrt{2}}}{2}$
点评 本题考查抛物线的定义、标准方程,以及简单性质的应用,考查点到直线的距离公式,判断当D,M,A三点共线时|MA|+|MD|最小是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.一个几何体的三视图如图所示,则此几何体的体积为( )
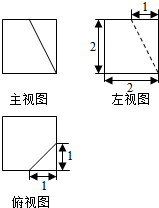

| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{23}{3}$ | D. | $\frac{22}{3}$ |
5.设a=e0.3,b=0.92,c=ln0.9,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<c<a |
6.最新高考改革方案已在上海实施,某教育行政主管部门为了解我省广大师生对新高考改革方案的看法,对我市某中学500名师生进行调查,统计结果如下:
从全体被调査师生中随机抽取1人,该人是“赞成改革”的学生的概率为0.3,且z=2y,
(1)现从全体被调查师生中分层抽样的方法抽取50名进行问卷调査,则应抽取“不赞成改革”的教师和学生人数各是多少?
(2)在(1)中所抽取的“不赞成改革”的人中,随机选出三人进行座谈,求至少有一名教师被选出的概率.
| 赞成改革 | 不赞成改革 | 无所谓 | |
| 教师 | 120 | y | 40 |
| 学生 | x | z | 130 |
(1)现从全体被调查师生中分层抽样的方法抽取50名进行问卷调査,则应抽取“不赞成改革”的教师和学生人数各是多少?
(2)在(1)中所抽取的“不赞成改革”的人中,随机选出三人进行座谈,求至少有一名教师被选出的概率.
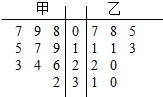 某赛季,甲、乙两名篮球运动员都参加了10场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是( )
某赛季,甲、乙两名篮球运动员都参加了10场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,若甲运动员的中位数为a,乙运动员的众数为b,则a-b的值是( )