题目内容
已知双曲线
：
的焦距为
，且经过点
。
(Ⅰ)求双曲线
的方程和其渐近线方程；
(Ⅱ)若直线
与双曲线
有且只有一个公共点,求所有满足条件的
的取值。
(Ⅰ) 
，
(Ⅱ) 
【解析】
试题分析：在解第一问的时候可以根据双曲线的定义，得出对应的
，再根据双曲线中
之间的关系，得出
的值，从而得出双曲线的方程；对于第二问，涉及到直线与双曲线的位置关系，取决于联立以后的方程的根的个数，注意对二次项系数的讨论，当二次项系数为0时的情况不要丢掉，只有一个公共点包括了相切的时候和与渐近线平行的时候.
试题解析：(1)由题意可知：双曲线的焦点为（-2, 0）和（2,0）
根据定义有
∴
，由以上可知：
．∴所求双曲线C的方程为：． 4分
渐近线方程为： 6分
(2)由
得：
. 7分
①当
即
时，此时直线
与双曲线相交有一个公共点，符合题意 8分
② 当
即
时，由△=0得
，
此时直线与双曲线相切有一个公共点，符合题意 11分
综上所述：符合题意的k的所有取值为。 12分
考点：双曲线的方程，双曲线的渐近线方程，直线与双曲线的位置关系.
练习册系列答案
优学名师名题系列答案
相关题目
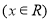的最小值为a.
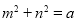，求
的最小值.
的解集是（ ）
B.
C.
D.
的图象可能是
，
”的否定形式是（ ）
，
B.
，
，
D.
，
，则
是直角三角形”的否命题的真假性为 
中，点
为上底面对角线
的中点，若
，则（ ）
B 
D 
，B=
，则
．
,
，则
的最小值是 .