题目内容
20. (本题满分16分)集合A是由具备下列性质的函数 组成的:
组成的:
(1)函数 的定义域是
的定义域是 ;
;
(2)函数 的值域是
的值域是 ;
;
(3)函数 在
在 上是增函数.试分别探究下列两小题:
上是增函数.试分别探究下列两小题:
(Ⅰ)判断函数 ,及
,及 是否属于集合A?并证明.
是否属于集合A?并证明.
(Ⅱ)对于(Ⅰ)中你认为属于集合A的函数 ,不等式
,不等式 是否对于任意的
是否对于任意的 总成立?若不成立,为什么?若成立,请证明你的结论.
总成立?若不成立,为什么?若成立,请证明你的结论.
(Ⅰ) 不属于集合A,
不属于集合A, 属于集合A;(Ⅱ)详见解析.
属于集合A;(Ⅱ)详见解析.
【解析】
试题分析:(Ⅰ)只需验证函数 是否满足3个条件即可,因为
是否满足3个条件即可,因为 为
为 上是增函数,所以
上是增函数,所以 的值域是
的值域是 ,不满足(2),不属于集合A(或举反例,如
,不满足(2),不属于集合A(或举反例,如 ,不满足(2));
,不满足(2)); 的定义域是
的定义域是 ,又
,又 为定义域上的增函数,所以函数
为定义域上的增函数,所以函数 的值域是
的值域是 ,满足条件(1)(2)(3),所以
,满足条件(1)(2)(3),所以 属于集合A;(Ⅱ)由(Ⅰ)知
属于集合A;(Ⅱ)由(Ⅰ)知 ,所以
,所以 所以不等式
所以不等式 对于任意的
对于任意的 总成立.
总成立.
试题解析:(Ⅰ)因为 为
为 上是增函数,所以
上是增函数,所以 的值域是
的值域是 ,函数
,函数 不属于集合A.(或
不属于集合A.(或 ,不满足条件)
,不满足条件)

 在集合A中,因为:函数
在集合A中,因为:函数 的定义域是
的定义域是 ;易知函数
;易知函数 在
在 上是增函数,所以函数
上是增函数,所以函数 的值域是
的值域是 ,满足条件(1)(2)(3)
,满足条件(1)(2)(3)
(Ⅱ)由(Ⅰ)知 ,
,

 ,
,
 对于任意的
对于任意的 总成立.
总成立.
考点:(Ⅰ)函数的基本性质;(Ⅱ)不等式证明.

练习册系列答案
相关题目
 ( )
( ) B.
B. C.
C. D.
D.
 满足,
满足, 目标函数是
目标函数是 ,则( )
,则( )
 ,
, 无最小值
无最小值 无最大值
无最大值 既无最大值,也无最小值
既无最大值,也无最小值 是双曲线上关于原点对称的两点,P是双曲线上的动点,直线PM,PN的斜率分别为
是双曲线上关于原点对称的两点,P是双曲线上的动点,直线PM,PN的斜率分别为 ,若
,若 的最小值为1,则双曲线的离心率为( )
的最小值为1,则双曲线的离心率为( ) B.
B. C.
C. D.
D.
 ,则目标函数
,则目标函数 的最大值是( )
的最大值是( )


 的值.
的值. 的最小值为
的最小值为  上一点
上一点 到焦点的距离为2,则点
到焦点的距离为2,则点 的横坐标是_____________.
的横坐标是_____________.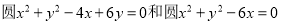 交于A,B两点,则AB的垂直平分线的方程为___________________.
交于A,B两点,则AB的垂直平分线的方程为___________________.