题目内容
(本小题满分13分)已知椭圆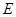 的中心在原点
的中心在原点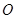 ,焦点
,焦点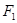 ,
,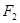 在
在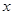 轴上,经过点
轴上,经过点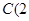 ,
,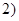 ,且抛物线
,且抛物线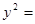
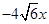 的焦点为
的焦点为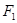 .
.
(1) 求椭圆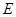 的方程;
的方程;
(2) 垂直于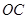 的直线
的直线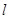 与椭圆
与椭圆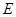 交于
交于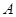 ,
,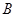 两点,当以
两点,当以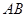 为直径的圆
为直径的圆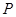 与
与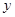 轴相切时,求直线
轴相切时,求直线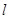 的方程和圆
的方程和圆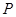 的方程.
的方程.
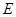 的中心在原点
的中心在原点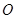 ,焦点
,焦点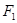 ,
,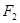 在
在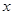 轴上,经过点
轴上,经过点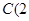 ,
,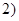 ,且抛物线
,且抛物线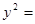
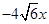 的焦点为
的焦点为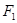 .
.(1) 求椭圆
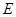 的方程;
的方程;(2) 垂直于
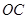 的直线
的直线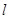 与椭圆
与椭圆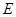 交于
交于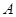 ,
,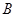 两点,当以
两点,当以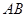 为直径的圆
为直径的圆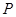 与
与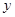 轴相切时,求直线
轴相切时,求直线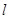 的方程和圆
的方程和圆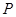 的方程.
的方程.(1)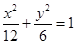
(2)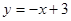 ,
,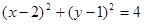 或
或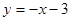 ,
,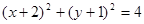
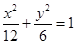
(2)
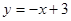 ,
,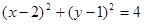 或
或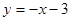 ,
,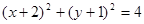
试题分析:(1) 设椭圆
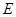 的方程为
的方程为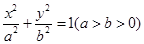 ,
,则由椭圆经过点
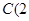 ,
,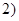 ,有
,有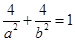 ,①
,①∵抛物线
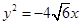 的焦点为
的焦点为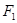 ,∴
,∴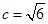 , ②
, ②又
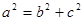 ③,
③,由①、②、③得
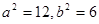 ,
,所以椭圆
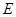 的方程为
的方程为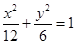 . ……5分
. ……5分(2) 依题意,直线
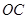 斜率为1,
斜率为1,由此设直线
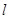 的方程为
的方程为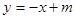 ,代入椭圆
,代入椭圆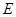 方程,得
方程,得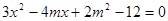 .
.由
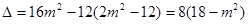 ,得
,得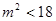 .
. 记
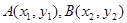 ,
,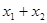 =
=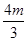 ,
,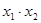 =
=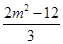 ,
,圆
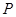 的圆心为
的圆心为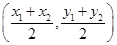 ,即
,即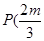 ,
, 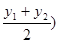 ,
,半径
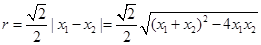
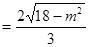 ,
,当圆
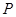 与
与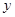 轴相切时,
轴相切时,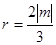
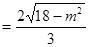 ,即
,即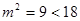 ,
,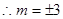 ,
,当
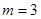 时,直线
时,直线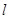 方程为
方程为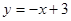 ,此时,
,此时,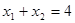 ,圆心为(2,1),半径为2,圆
,圆心为(2,1),半径为2,圆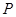 的方程为
的方程为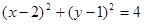 ;
;同理,当
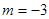 时,直线
时,直线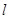 方程为
方程为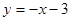 ,
,圆
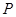 的方程为
的方程为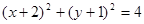 . ……13分
. ……13分点评:每年高考圆锥曲线问题都出现在压轴题的位置上,难度一般较大,要充分利用数形结合数学思想方法,尽可能的寻求简单方法,尽可能的减少运算,另外思维一定要严谨,运算一定要准确.

练习册系列答案
相关题目
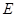 :
: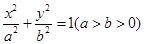 的左、右焦点分别为
的左、右焦点分别为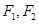 ,焦距为2,,过
,焦距为2,,过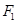 作垂直于椭圆长轴的弦长
作垂直于椭圆长轴的弦长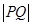 为3.
为3. 求椭圆
求椭圆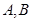 两点.并判断是否存在直线l使得
两点.并判断是否存在直线l使得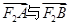 的夹角为钝角,若存在,求出l的斜率k的取值范围。
的夹角为钝角,若存在,求出l的斜率k的取值范围。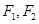 是离心率为
是离心率为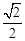 的椭圆,
的椭圆,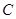 :
: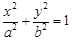 (
(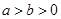 )的左、右焦点,直线
)的左、右焦点,直线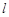 :
: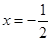 将线段
将线段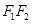 分成两段,其长度之比为1 : 3.设
分成两段,其长度之比为1 : 3.设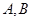 是
是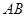 的中点
的中点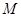 在直线
在直线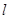 上,线段
上,线段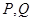 两点.
两点.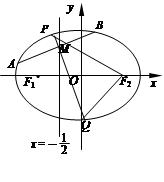
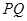 为直径的圆经过点
为直径的圆经过点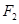 ,若存在,求出
,若存在,求出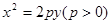 过点
过点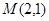 .
.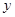 轴上的圆
轴上的圆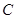 过点
过点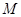 的切线恰是抛物线在点
的切线恰是抛物线在点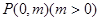 为
为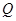 是点
是点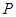 关于原点的对称点,过点
关于原点的对称点,过点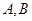 两点,若
两点,若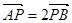 ,证明:
,证明: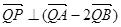 .
.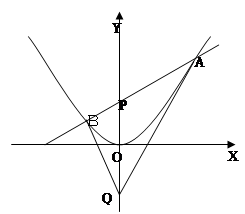
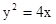 上一点
上一点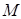 到焦点的距离为1,则点
到焦点的距离为1,则点



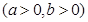 的离心率为
的离心率为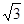 ,且它的一条准线与抛物
,且它的一条准线与抛物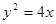 的准线重合,则此双曲线的方程是( )
的准线重合,则此双曲线的方程是( )



 与曲线
与曲线 相切于点
相切于点 ,则
,则 的值为 ( )
的值为 ( )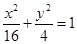 内一点(2,1)的弦被该点平分,则该弦所在直线的方程是_______________.
内一点(2,1)的弦被该点平分,则该弦所在直线的方程是_______________.