题目内容
(本题满分13分) 如图,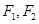 是离心率为
是离心率为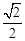 的椭圆,
的椭圆,
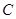 :
: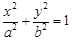 (
(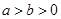 )的左、右焦点,直线
)的左、右焦点,直线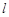 :
: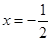 将线段
将线段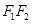 分成两段,其长度之比为1 : 3.设
分成两段,其长度之比为1 : 3.设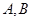 是
是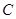 上的两个动点,线段
上的两个动点,线段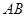 的中点
的中点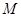 在直线
在直线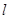 上,线段
上,线段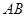 的中垂线与
的中垂线与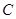 交于
交于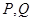 两点.
两点.
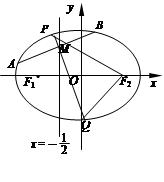
(Ⅰ) 求椭圆C的方程;
(Ⅱ) 是否存在点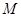 ,使以
,使以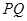 为直径的圆经过点
为直径的圆经过点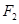 ,若存在,求出
,若存在,求出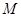 点坐标,若不存在,请说明理由.
点坐标,若不存在,请说明理由.
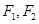 是离心率为
是离心率为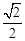 的椭圆,
的椭圆,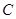 :
: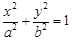 (
(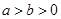 )的左、右焦点,直线
)的左、右焦点,直线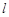 :
: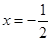 将线段
将线段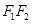 分成两段,其长度之比为1 : 3.设
分成两段,其长度之比为1 : 3.设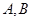 是
是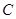 上的两个动点,线段
上的两个动点,线段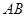 的中点
的中点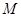 在直线
在直线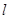 上,线段
上,线段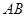 的中垂线与
的中垂线与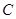 交于
交于 两点.
两点.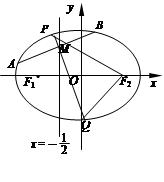
(Ⅰ) 求椭圆C的方程;
(Ⅱ) 是否存在点
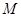 ,使以
,使以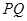 为直径的圆经过点
为直径的圆经过点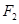 ,若存在,求出
,若存在,求出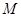 点坐标,若不存在,请说明理由.
点坐标,若不存在,请说明理由.(Ⅰ)  (Ⅱ)存在两点
(Ⅱ)存在两点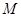 符合条件,坐标为
符合条件,坐标为 ,理由见解析
,理由见解析
 (Ⅱ)存在两点
(Ⅱ)存在两点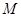 符合条件,坐标为
符合条件,坐标为 ,理由见解析
,理由见解析试题分析:(Ⅰ) 设
 ,则
,则 =
= ,所以
,所以 =1.
=1.因为离心率e=
 ,所以
,所以 =
=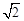 .
.所以椭圆C的方程为
 . ……5分
. ……5分(Ⅱ) 当直线
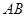 垂直于
垂直于 轴时,直线
轴时,直线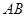 方程为
方程为 =-
=- ,
,此时
 (
( ,0)、
,0)、 (
( ,0) ,
,0) , .不合题意; ……7分
.不合题意; ……7分当直线
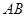 不垂直于
不垂直于 轴时,设存在点
轴时,设存在点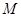 (-
(- ,
, ) (
) ( ≠0),直线
≠0),直线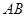 的斜率为
的斜率为 ,
,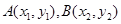 .
.由
 得
得 =0,则
=0,则 ,
,故
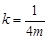 .此时,直线
.此时,直线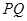 斜率为
斜率为 ,
,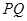 的直线方程为
的直线方程为 .
.即
 .
.联立
 消去
消去 ,整理得
,整理得 .
.所以
 ,
, . ……10分
. ……10分由题意
 0,于是
0,于是


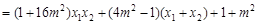

 =0.
=0.
因为
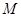 在椭圆内,
在椭圆内,
 符合条件;
符合条件;综上,存在两点
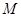 符合条件,坐标为
符合条件,坐标为 . ……13分
. ……13分点评:设直线方程时,要考虑到直线方程斜率是否存在;对于探究性问题,可以先假设存在,再进行计算,如果能求出来,就说明存在,如果求不出来或者得出矛盾,则说明不存在.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
 的焦点F,与抛物线交于两点A,B,
的焦点F,与抛物线交于两点A,B,
 的方程;
的方程; 的面积S的最大值;
的面积S的最大值; +
+ =1的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,求弦AB的长_______
=1的右焦点作一条斜率为2的直线与椭圆交于A、B两点,O为坐标原点,求弦AB的长_______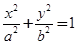 (
(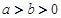 )的两焦点分别为
)的两焦点分别为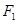 、
、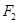 ,以
,以



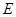 的中心在原点
的中心在原点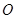 ,焦点
,焦点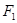 ,
,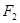 在
在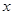 轴上,经过点
轴上,经过点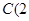 ,
,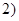 ,且抛物线
,且抛物线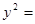
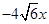 的焦点为
的焦点为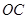 的直线
的直线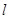 与椭圆
与椭圆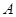 ,
,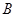 两点,当以
两点,当以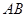 为直径的圆
为直径的圆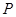 与
与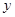 轴相切时,求直线
轴相切时,求直线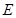 的对称轴为坐标轴,焦点在
的对称轴为坐标轴,焦点在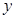 轴上,离心率
轴上,离心率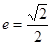 ,
,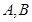 分别为椭圆的上顶点和右顶点,且
分别为椭圆的上顶点和右顶点,且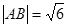 .
.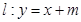 与椭圆
与椭圆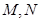 两点,且
两点,且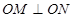 (其中
(其中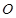 为坐标原点),求
为坐标原点),求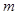 的值.
的值.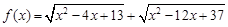 的最小值为 .
的最小值为 .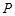 在曲线
在曲线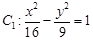 上,点
上,点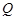 在曲线
在曲线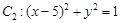 上,点
上,点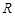 在曲线
在曲线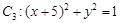 上,则
上,则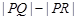 的最大值是 .
的最大值是 .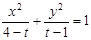 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题: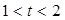 ,则C表是长轴在x轴上的椭圆.
,则C表是长轴在x轴上的椭圆. 上的一点,
上的一点, 、
、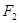 为该椭圆的两个焦点,若
为该椭圆的两个焦点,若 ,则
,则 的面积等于( )
的面积等于( )