题目内容
若过椭圆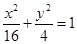 内一点(2,1)的弦被该点平分,则该弦所在直线的方程是_______________.
内一点(2,1)的弦被该点平分,则该弦所在直线的方程是_______________.
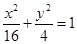 内一点(2,1)的弦被该点平分,则该弦所在直线的方程是_______________.
内一点(2,1)的弦被该点平分,则该弦所在直线的方程是_______________. .
.试题分析:设弦AB的两个端点
 ,则
,则 ,
, 两式作差变形可得
两式作差变形可得 ,所以该弦所在直线的方程为
,所以该弦所在直线的方程为 ,即
,即 .
.点评:对于焦点在x轴的椭圆根据点差法整理后得到的式子为
 ,由此根据弦点的坐标,可求出弦所在直线的斜率进而得到所求直线的方程.
,由此根据弦点的坐标,可求出弦所在直线的斜率进而得到所求直线的方程.
练习册系列答案
相关题目
题目内容
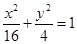 内一点(2,1)的弦被该点平分,则该弦所在直线的方程是_______________.
内一点(2,1)的弦被该点平分,则该弦所在直线的方程是_______________. .
. ,则
,则 ,
, 两式作差变形可得
两式作差变形可得 ,所以该弦所在直线的方程为
,所以该弦所在直线的方程为 ,即
,即 .
. ,由此根据弦点的坐标,可求出弦所在直线的斜率进而得到所求直线的方程.
,由此根据弦点的坐标,可求出弦所在直线的斜率进而得到所求直线的方程.