题目内容
已知首项不为零的数列{an}的前n项和为Sn,若对任意的r,t∈N*,都有| Sr |
| St |
| r |
| t |
(Ⅰ)判断数列{an}是否为等差数列,并证明你的结论;
(Ⅱ)若数列{bn}的第n项bn是数列{an}的第bn-1项(n≥2,n∈N*),且a1=1,b1=3,求数列{bn}的前n项和Tn.
分析:(I)因为已知前n项和可求得通项用通项公式法判断;
(II)由(I)知an=2n-1,则根据题意得出bn与bn-1间的关系,构造等比数列bn-1,求得bn进而求得Tn
(II)由(I)知an=2n-1,则根据题意得出bn与bn-1间的关系,构造等比数列bn-1,求得bn进而求得Tn
解答:解:(Ⅰ)令t=1,r=n,得
=n2,于是Sn=n2a1.
当n≥2时,an=Sn-Sn-1=(2n-1)a1;
当n=1时,S1=a1也适合上式.
综上知,an=(2n-1)a1.
所以an-an-1=2a1.
故数列{an}是公差d=2a1的等差数列.
(Ⅱ)当a1=1时,由(Ⅰ)知,an=2n-1.
于是bn=2bn-1-1,即bn-1=2(bn-1-1).
因此数列{bn-1}是首项为b1-1=2,公比为2的等比数列,所以bn-1=2×2n-1=2n.即bn=2n+1.
故Tn=b1+b1++bn=( 21+22++2n )+n=
+n=2n+1+n-2.
| Sn |
| S1 |
当n≥2时,an=Sn-Sn-1=(2n-1)a1;
当n=1时,S1=a1也适合上式.
综上知,an=(2n-1)a1.
所以an-an-1=2a1.
故数列{an}是公差d=2a1的等差数列.
(Ⅱ)当a1=1时,由(Ⅰ)知,an=2n-1.
于是bn=2bn-1-1,即bn-1=2(bn-1-1).
因此数列{bn-1}是首项为b1-1=2,公比为2的等比数列,所以bn-1=2×2n-1=2n.即bn=2n+1.
故Tn=b1+b1++bn=( 21+22++2n )+n=
| 2 ( 1-2n ) |
| 1-2 |
点评:本题主要考查an与Sn的关系,等差数列,等比数列等基础知识,同时考查分析问题和解决问题的能力

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
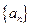 的前n项和为
的前n项和为 ,若对任意的r、s
,若对任意的r、s ,都有
,都有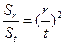 .
.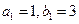 ,数列
,数列 的第n项是数列
的第n项是数列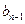 项
项 ,求
,求 ;
; .
. 的前
的前 项和为
项和为 ,若对任意的
,若对任意的 ,
, ,都有
,都有 .
. 的第
的第 是数列
是数列 项
项 ,且
,且 ,
, ,求数列
,求数列 .
.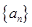 的前n项和为
的前n项和为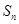 ,若对任意的r、s
,若对任意的r、s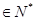 ,都有
,都有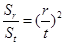 .
.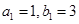 ,数列
,数列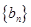 的第n项是数列
的第n项是数列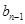 项
项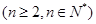 ,求
,求 ;
;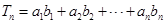 .
.