题目内容

10．一个人把4根细绳紧握在手中，仅露出它们的头和尾，然后另一人每次任取一个绳头和一个绳尾打结，依次进行直到打完4个结，则放开手后4根细绳恰巧构成4个环的概率为$\frac{1}{16}$．

分析 先求出基本事件总数n=${C}_{4}^{1}{C}_{4}^{1}$=16，由此能求出放开手后4根细绳恰巧构成4个环的概率．

解答 解：一个人把4根细绳紧握在手中，仅露出它们的头和尾，
然后另一人每次任取一个绳头和一个绳尾打结，依次进行直到打完4个结，
基本事件总数n=${C}_{4}^{1}{C}_{4}^{1}$=16，
∴放开手后4根细绳恰巧构成4个环的概率为：p=$\frac{1}{16}$．
故答案为：$\frac{1}{16}$．

点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．

练习册系列答案
相关题目
20．已知F1（-1，0），F2（1，0）分别是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{3}$=1（a＞0）的左、右焦点．
（Ⅰ）求椭圆C的方程；
（Ⅱ）若A，B分别在直线x=-2和x=2上，且AF1⊥BF1．
（ⅰ） 当△ABF1为等腰三角形时，求△ABF1的面积；
（ⅱ） 求点F1，F2到直线AB距离之和的最小值．
1．某校高三年级要从5名男生和2名女生中任选3名代表参加数学竞赛（每人被选中的机会均等），则在男生甲被选中的情况下，男生乙和女生丙至少一个被选中的概率是$\frac{3}{5}$．
18．在△ABC中，角A，B，C所对的边分别为a，b，c，△ABC的面积为S，$asinB=\sqrt{3}bcosA$．
（1）求角A的大小；
（2）若$a=\sqrt{3}$，$S=\frac{{\sqrt{3}}}{2}$，求b+c的值．
5．在坐标系中，圆C的圆心在极轴上，且过极点和点（3$\sqrt{2}$，$\frac{π}{4}$），求圆C的极坐标方程．
15．已知$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（4，2），则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角的余弦值为$\frac{4}{5}$．
2．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（$\sqrt{2}$，1），以原点为圆心，椭圆短半轴长为半径的圆经过椭圆的焦点．
（1）求椭圆C的方程；
（2）设过点（-1，0）的直线l与椭圆C相交于A、B两点，试问在x轴上是否存在一个定点M，使得$\overrightarrow{MA}$•$\overrightarrow{MB}$恒为定值？若存在，求出该定值及点M的坐标；若不存在，请说明理由．
19．已知i为虚数单位，则复数z=（1+i）i对应的点位于（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
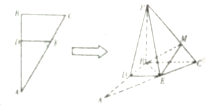20．如图，在△ABC中，AB⊥BC，点D，E分别在AB，AC上，AD=2DB，AC=3EC，沿DE将△ADE翻折起来，使得点A到P的位置，满足$PB=\sqrt{3}BD$．
（1）证明：DB⊥平面PBC；
（2）若$PB=BC=\sqrt{3}，PC=\sqrt{6}$，点M在PC上，且，求三棱锥P-BEM的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网