题目内容
10．“k=1”是“函数$f（x）=\frac{{k-{e^x}}}{{1+k{e^x}}}$（k为常数）在定义域上是奇函数”的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 函数$f（x）=\frac{{k-{e^x}}}{{1+k{e^x}}}$（k为常数）在定义域上是奇函数，则f（-x）+f（x）=0，化为：k2=1，解出即可判断出结论．
解答 解：函数$f（x）=\frac{{k-{e^x}}}{{1+k{e^x}}}$（k为常数）在定义域上是奇函数，则f（-x）+f（x）=0，
∴$\frac{k-{e}^{-x}}{1+k{e}^{-x}}$+$\frac{k-{e}^{x}}{1+k{e}^{x}}$=0，
化为：k2（ex+e-x）=ex+e-x，
∴k2=1，
解得k=±1，经过验证，此时函数f（x）是奇函数．
∴“k=1”是“函数$f（x）=\frac{{k-{e^x}}}{{1+k{e^x}}}$（k为常数）在定义域上是奇函数”的充分不必要条件．
故选：A．
点评 本题考查了函数的性质、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
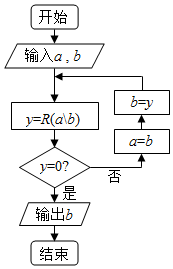“辗转相除法”的算法思路如图所示，记R（a\b）为a除以b所得的余数（a，b∈N*），执行如图的程序框图，若输入a，b分别为405，75，则输出b的值为（ ）