题目内容
19.若数列{an}为等比数列,则在下列4个命题中,真命题的个数是( )①{${a}_{n}^2$}也是等比数列;
②{can}(c≠0)也是等比数列;
③{$\frac{1}{{a}_{n}}$}也是等比数列;
④{lnan}也是等比数列.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 设出等比数列{an}的首项和公比,由等比数列的定义说明①②③为等比数列,举反例说明④不是等比数列
解答 解:数列{an}是等比数列,设首项为a1,公比为q,则an=a1qn-1,
对于①,an2=a12q2(n-1),∴{${a}_{n}^2$}是以a12为首项,q2为公比的等比数列;
对于②,c≠0时,can=ca1•qn-1,∴{can}是以ca1为首项,q为公比的等比数列;
对于③,$\frac{1}{{a}_{n}}$=$\frac{1}{{a}_{1}{•q}^{n-1}}$=$\frac{1}{{a}_{1}}$•$\frac{1}{{q}^{n-1}}$,∴{$\frac{1}{{a}_{n}}$}是以$\frac{1}{{a}_{1}}$为首项,$\frac{1}{q}$为公比的等比数列;
对于④,当数列{an}存在负项时,此时lgan无意义,故{lgan}不是等比数列;
综上,是等比数列的为①②③共3个.
故选:B.
点评 本题考查了等比数列的概念与应用问题,熟练掌握等比数列的定义是解题的关键,是基础题目.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
10.“k=1”是“函数$f(x)=\frac{{k-{e^x}}}{{1+k{e^x}}}$(k为常数)在定义域上是奇函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.下列说法正确的是( )
| A. | “a2>9”是“a>3”的充分不必要条件 | |
| B. | “?x0∈R,使得$sin{x_0}+\frac{2}{{sin{x_0}}}>2\sqrt{2}$”的否定是“$?x∈R,sinx+\frac{2}{sinx}<2\sqrt{2}$” | |
| C. | 若A∧B是假命题,则A∨B是假命题 | |
| D. | “若a<0,则x2+ax+a<0有解”的否命题为“若a≥0,则x2+ax+a<0无解” |
4.若|cosθ|=-cosθ,|tanθ|=-tanθ,则θ终边在( )
| A. | 第一象限或x轴正半轴上 | B. | 第二象限或x轴负半轴上 | ||
| C. | 第三象限 | D. | 第四象限 |
11.已知sinθ>0,tanθ<0,则θ是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
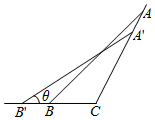 在△ABC中,角A、B、C所对的边分别是a、b、c.若∠C=$\frac{2}{3}$π,a、b、c依次成等差数列,且公差为2,如图.A′B′分别在射线CA,CB上运动,且满足A′B′=AB,设∠A′B′C′=θ,则△A′CB′周长最大值为7+$\frac{14\sqrt{3}}{3}$.
在△ABC中,角A、B、C所对的边分别是a、b、c.若∠C=$\frac{2}{3}$π,a、b、c依次成等差数列,且公差为2,如图.A′B′分别在射线CA,CB上运动,且满足A′B′=AB,设∠A′B′C′=θ,则△A′CB′周长最大值为7+$\frac{14\sqrt{3}}{3}$.